Let $F$ be an arbitrary bounded set on the plane, $n \in \mathbb{N}$.
Let's define $d_n(F)$ as the minimum diameter one can ensure when cutting a set $F$ into $n$ pieces.
So, here is a discussion of the value $d_n(F)$ for an arbitrary set of diameter 1.
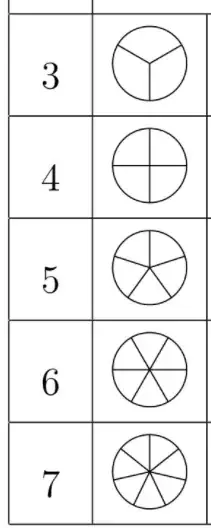
I decided to consider $d_n$ for a circle of unit diameter D. It is quite simple to understand the values of $d_n(D)$ for $n \leqslant 7$ and they are calculated in [SCY, page 96-98](Geometrical estimations and combinatorial geometry problems): $d_1(D) = d_2(D) = 1, d_3(D)= \frac{\sqrt 3}{2}, d_4(D) = \frac{ \sqrt 2}{2}, d_5(D) = \sin(\frac{\pi}{5})$, and $d_6(D) = d_7(D) = \frac{1}{2}$. I also can prove that $d_8 (D) = \sin(\frac{\pi}{7})$, this is also not difficult (there will be 1 set to cover the center and 7 to cover the border of disk)
But for $d_{9}(D)$ I don't know precise value. I know that $0.3826... = \sin(\frac{\pi}{8}) \leqslant d_9(D) \leqslant \frac{\sqrt{7} - 1}{3\sqrt{2}} = 0.3879...$.
The lower estimate is correct, because otherwise, for $x < \sin(\frac{\pi}{8})$, there are not enough 8 sets to cover the boundary of the disk, so the set that covers the center will have a diameter of at least $0.5$.
The upper bound is correct from this picture:
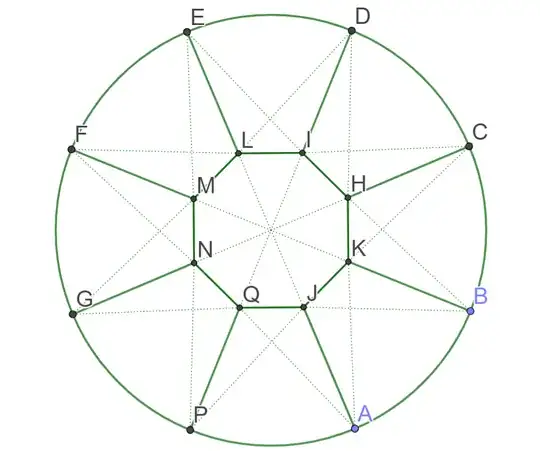
The dashed lines indicate the segments where the diameter is reached.
I think that this partition is optimal, but I don't yet understand how to prove it strictly. Does anyone have any ideas?