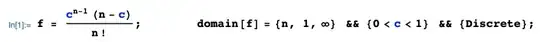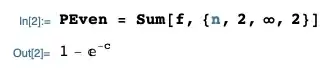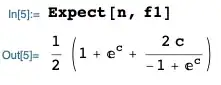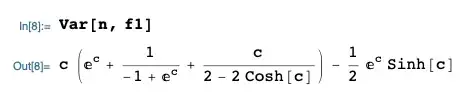An interesting stopping time problem using PGF's

Question

This is a question I thought of the other day:

Suppose $U_1, U_2, U_3, \cdots \overset{\text{iid}}{\sim} \text{Uniform}(0, 1)$ and let $N = \min\{n: \sum_{i=1}^{n}U_i \ge 1\}$. Compute $\mathbb{P}(N \in 2\mathbb{Z})$ (i.e. probability $N$ is even). How about $\mathbb{P}(N \in 3 \mathbb{Z})$? In general, $\mathbb{P}(N \in k\mathbb{Z})$. Similarly, what is $\mathbb{E}[N|N \in k\mathbb{Z}]$?

I'll post the answer below, but challenge yourself before looking!

Tom Chen · Accepted Answer · 2021-02-15T16:13:01.843

We are going to need a few results to answer this question.

Definition The probability generating function (PGF) of a random variable $X$ with support $\mathbb{N}_0 = \{0, 1, 2, \cdots\}$ is defined as $g_X(s) = \mathbb{E}[s^X]$.

Fact 1 By definition, \begin{align*} g_X(s) = \sum_{k=0}^{\infty} \mathbb{P}(X = k)s^k \end{align*}

Fact 2 We have \begin{align*} H_X(s) \overset{\text{def}}{=}\frac{1-g_X(s)}{1-s} = \sum_{k=0}^\infty\mathbb{P}(X > k)s^k \end{align*}

Fact 3 We have \begin{align*} \mathbb{P}(X \in k\mathbb{Z}) = \frac{1}{k}\sum_{j=0}^{k-1}g_X(\omega_{k,j}) \end{align*} where $\omega_{k,j} = \exp\left(\frac{2j\pi \mathbf{i}}{k}\right)$ are the $k$th roots of unity, with $\mathbf{i}$ being the imaginary unit.

Now we can attack this problem. First, note that \begin{align*} \mathbb{P}(N > n) = \mathbb{P}\left(\sum_{k=1}^{n}X_k < 1\right) = \frac{1}{n!} \end{align*} Since the probability corresponds to finding the volume of an $n$-dimensional right tetrahedron with leg side lengths 1. So we have \begin{align*} H_N(s) = \sum_{k=0}^{\infty}\mathbb{P}(N > k)s^k = e^s \end{align*} And therefore $g_N(s) = 1 - (1-s)H_N(s) = 1 - (1-s)e^s$. We can now see that \begin{align*} \mathbb{P}(N \in 2\mathbb{Z}) &= \frac{1 + g_N(-1)}{2} = 1 - e^{-1} \approx 0.6321 \\ \mathbb{P}(N \in 3\mathbb{Z}) &= \frac{1 + g_N(\exp(2\pi \mathbf{i}/3)) + g_N(\exp(4\pi \mathbf{i}/3))}{3} = 1 - \frac{\sin\left(\frac{\sqrt{3}}{2}\right)}{\sqrt{3e}} - \frac{\cos\left(\frac{\sqrt{3}}{2}\right)}{\sqrt{e}} \approx 0.3403 \\ \mathbb{P}(N \in 4\mathbb{Z}) &= \frac{1 + g_N(\mathbf{i}) + g_N(-1) + g_N(-\mathbf{i})}{4} = 1 - \frac{1}{2}e^{-1} - \frac{\sin(1)}{2} - \frac{\cos(1)}{2}\approx 0.1252 \\ &\vdots \end{align*} and so on. For expected values, we use the formula that \begin{align*} \mathbb{E}[N|N \in k\mathbb{Z}] = \frac{\sum_{n \in k\mathbb{N}_0}n \mathbb{P}(N = n)}{\mathbb{P}(N \in k\mathbb{Z})} \end{align*} Define \begin{align*} L_N(s) = \sum_{n = 0}^\infty n \mathbb{P}(N = n) s^n \end{align*} Note that $L_N(s) = s \frac{d}{ds} g_N(s) = s^2 e^s$ and \begin{align*} \sum_{n \in k\mathbb{N}_0}n \mathbb{P}(N = n) = \frac{1}{k} \sum_{j=0}^{k-1} L_N(\omega_{k,j}) \end{align*} Plugging in these values, we have \begin{align*} \mathbb{E}[N|N \in 2\mathbb{Z}] &= \frac{\frac{1}{2}(e^1 + e^{-1})}{1 - e^{-1}} \approx 2.44 \\ \mathbb{E}[N|N \in 3\mathbb{Z}] &= \frac{\frac{e}{3} + \frac{2 \sin(\frac{\sqrt{3}}{2} - \frac{\pi}{6})}{3\sqrt{e}}}{1 - \frac{\sin\left(\frac{\sqrt{3}}{2}\right)}{\sqrt{3e}} - \frac{\cos\left(\frac{\sqrt{3}}{2}\right)}{\sqrt{e}}} \approx 3.06 \\ \mathbb{E}[N|N \in 4\mathbb{Z}] &= \frac{\frac{1}{4}e^{-1} + \frac{1}{4}e - \frac{\cos(1)}{2}}{1 - \frac{1}{2}e^{-1} - \frac{\sin(1)}{2} - \frac{\cos(1)}{2}} \approx 4.0055 \end{align*} and so on.

Challenge Do the same thing to compute $\text{Var}(N|N \in k \mathbb{Z})$.

wolfies · Answer 2 · 2021-02-15T18:04:13.593

Here is a more general solution for any stopping point $0 <c \le 1$ that nests the special case of $c = 1$ posed in the question.

As set out at Random sums of iid Uniform random variables, by simple geometric construction, the cdf of the number $N$ of draws required to exceed $c$, for $0<c \le 1$, is: $P(N \leq n) = 1 - \large \frac{c^n}{n!}$.

Then the pmf of $N$ is $f(n)$: