16

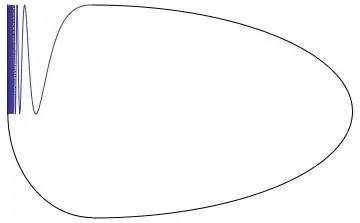
The Warsaw Circle is defined as the closed topologist's sine curve, with an additional arc attached at its free end point and one of the end points of the critical line:

enter image description here

Since we don't have an uncountable collection of disjoint open sets in the plane - such as the bounded component of its complement - we'll have to have an uncountable sequence $W_r$ such that if $r < s$ then $W_r$ is contained in the bounded component of $W_s^c$. Trying to draw it, it's actually kind of hard for me to tell for sure if it's true or not; it LOOKS true, but jeeze I think showing it with analytic, coordinate representations of each one is gonna be a bear.

Anyone really feeling it?

To be honest, I don't know the answer for the closed topologist's sine curve itself, either! Probably both are possible or both are impossible; have never seen it proved for either space.

John Samples
  • 481
  • 1
    My gut feeling is that it should be impossible. If you have a Warsaw circle W in your plane, then you might be able to show that any small perturbation of W (where by "perturbation" I mean moving around, shrinking, or growing without altering the shape) is going to intersect with your W. I feel like that should suffice to prove impossibility. – Jeroen van der Meer Jan 30 '21 at 19:28
  • That was my strong, initial impression as well - the 'countable' nature of the divots won't allow a Cantor Set of them to mesh. But after playing with it I'm unsure. You can get a pair arbitrarily close to each other; take the one as in the picture, then wrap your copy around it on the outside so that the limit arc is slightly to the left, and slightly higher, than the inner one. Jam the limit arc (and the tail of the wiggle) of the inner one into an arbitrarily close 'divot' of the outer. This procedure 'smooths out' the bigger one a bit. It's close, but the shape changes - as u suggest. – John Samples Jan 30 '21 at 20:20
  • I have a feeling that it's true iff there are uncountably many disjoint topologist's sine curves. The Moore Theorem (no uncountable collection of disjoint triods) is maybe the best shot at a "slick" proof of impossibility, somehow extending it using the fact that these continua don't actually contain triods, but the topologist's sine curve is (simple-triod)-like. – John Samples Jan 30 '21 at 20:23
  • "I have a feeling that it's true iff there are uncountably many disjoint topologist's sine curves." Surely there are, right? With respect to your picture, just stack them vertically. – Jeroen van der Meer Jan 30 '21 at 20:34
  • But then their critical arcs won't be disjoint from each other - I meant closed topologist's sine curves if that's the issue, sorry. But yeah, "stack them vertically - with a little bit of leftward shift as you do it" is the procedure that looks maybe-doable (for either space). I mean basically that's the only way to do it; trying to rotate the limit arc around won't help out; since it's an uncountable family, we can pick out an uncountable collection where the critical arcs all have nearly the same endpoints using pigeonhole and rational approximation of the end points. – John Samples Jan 30 '21 at 20:40
  • 1
    All I can say is that it is a real cool problem: I keep changing my mind about its truth. It reminds me about the covering-the-plane-with-disks problem I proposed here: https://mathoverflow.net/questions/8247/one-step-problems-in-geometry/380224?noredirect=1#comment965726_380224 – Andrea Marino Jan 31 '21 at 03:00
  • Nevertheless, I think the construction is possible. Keep track ( on a line ) the x-coordinates of the "left-upper" vertices of the warsaw circles I am going to describe you. Take one circle. For any "hole", put a circle in there (this is possible). This defines a configuration $C_1$. The x-coord of vertices here resembles the sequence ${1/n} \cup {0}$. For any new warsaw circle, put $\mathbb{N}$ circles in the holes as above. This defines $C_2$. Define $C_{\lambda} $ by transfinite induction. I think the x-coord of the vertices in $C_{\omega_1}$ are a perfect set, thus uncountable. – Andrea Marino Jan 31 '21 at 03:10
  • @AndreaMarino - What "transfinite induction" are you referring to? Over what well-ordered set? In what you've described, the new circles are all fit in a previous circle, and you can only accomplish this decreasing of size a countable number of times. By this construction, each circle has a finite number of other circles it is inside, and at each depth of inclusion, there are only a countable number of circles. The result will be countable. – Paul Sinclair Jan 31 '21 at 05:33
  • The transfinite induction I am referring to is to define an increasing set of circles. $C_{n+1}$ is defined as above: you take the circles in $C_{n}\setminus C_{n-1}$ and you apply the construction above to each one. I think I didn't explain this passage well: the new circles $W_1, \ldots, W_n, \ldots $ in $W$ are such that $W_1 \to W_2 \to \ldots \to W_n \to \ldots $ and $W_i \to W$, where the relation $\to$ means "the interior of the first is contained in the interior of the second. If they were topologist's sine curves no shrink would be needed. The problem I am seeing now is the y-shift.. – Andrea Marino Jan 31 '21 at 11:20
  • Also, it is not evident how to continue from a limit ordinal $C_{\lambda}$ and this is where the problems you were mentioning are hidden. But if we manage to do this passage and understand where to put the new circles... Once you arrive to an uncountable ordinal (eg $\omega_1$) you are done because at each step you added at least one circle. btw, even if the construction I made does not works, the inductive step (not really easy to depict!) shows how to draw "accumulating circles". My question is: how do you construct a perfect set on the real line starting from a point and adding new points? – Andrea Marino Jan 31 '21 at 11:32
  • Trying to use the Moore Theorem as I suggested will not work. I asked my friend about the more general problem of tree-like continua, and actually he had written a paper giving an example of a simple-triod-like continuum with uncountably many disjoint copies in the plane. It's a fairly difficult paper but you can get through it if you want: https://www.semanticscholar.org/paper/An-uncountable-family-of-copies-of-a-non-chainable-Hoehn-Hoehn/e50bf209e7164f5930357cafa2e59bb669503a34 – John Samples Jan 31 '21 at 20:37
  • Waiting on authoritative answer from him, but I'm back to "not doable." Sketch: Use separability, approximate end points of critical lines $C_r$ of $W_r$ with end points $p_r, q_r$ and get an uncountable collection that are all close. Take a Cantor set so continuity gets trivial, to isotope the plane so they all have nearly the same length/angle. In $W_r$ let $a_r^n \rightarrow p_r, b_r^n \rightarrow q_n$. If $W_r$ is outside $W_s$ then $W_r$ jumps over $W_s$ (relative to $x$-coordinate if chosen "coherently") "after only finitely many $p_r^n$." But that's for any pair, not possible. – John Samples Jan 31 '21 at 21:36
  • You can always take a Cantor set of them due to a theorem mentioned in the intro to that paper I linked, btw^ The hard part here is what does "coherently" mean, because the "wiggles" ostensibly are allowed to behave quite differently from each other as $r$ changes. For example, look up a space called the M-continuum. Trying to use the $x$-coordinates of the $p_r^n$'s means you'll want to make sure that the $p_r$ are 'in order', i.e. they're not spiraling basically (same for $q_r$'s ofc). This sketch should work IMO. – John Samples Jan 31 '21 at 21:47
  • Most likely, there is such a family, but why do you care? Incidentally, there is a foliation of the annulus by pseudo-circles, which are connected continua much worse than the Warsaw circles (each separates the plane in exactly two components, is compact, connected and contains no nondegenerate subacrs). What's worse (or better, it depends) is the fact that such foliations do appear naturally when one studies certain smooth dynamical systems. – Moishe Kohan Feb 04 '21 at 23:05
  • 1
    True, but there are also foliations with pseudo-arcs - but not simple triods. So this observation doesn't give me a really strong feeling about it. The only reason I care about this example in particular is because I'd like to see how a proof would look, tbh Then maybe I will have ideas for more 'interesting' problems. – John Samples Feb 05 '21 at 00:37

1 Answers1

5

Yes, there exists such a collection. Any arc-like or circle-like planar continuum (all arc-like continua are planar) admits a mutually disjoint, uncountable collection of copies of itself in the plane. The proof is a bit long but elementary: https://link.springer.com/article/10.1007/BF01696773

Logan Hoehn has given an example of a tree-like continuum which is not arc-like and also admits uncountably many mutually disjoint copies in the plane. It's harder but still readable: https://uts.nipissingu.ca/loganh/CopiesOfX.pdf

A classification of continua which admit such embeddings is not known, and there isn't any generally accepted "main conjecture" on the problem. There's a broad feeling that if current tools are sufficient for such a classification then it will center around one of the various notions of 'span.'

John Samples
  • 481