Can an equilateral triangle be dissected into 5 congruent convex pieces?

Question

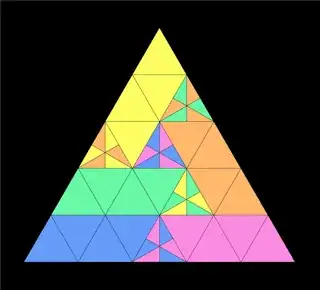
There is a rather surprising dissection of an equilateral triangle into 5 congruent pieces:

                                                   

However, these pieces aren't very "nice", consisting of 2 or 6 connected components depending on how one counts single-point overlaps.

I expect that the analogous question for arbitrary connected pieces is quite difficult, but I wonder if the case of convex pieces is sufficiently restricted to allow for a proof of impossibility (which I strongly suspect is the case).

One aspect of this problem that makes it much more tractable is that the pieces have to be polygons, because any border between two pieces must be a straight line to preserve convexity of both pieces.

In fact, this analysis can be extended a little further to show that the pieces have at most 5 sides. The number of edges on a piece is at most the number of edges of the triangle it touches, plus the number of other pieces it touches. $K_5$ is non-planar, so there is a piece touching at most 3 others. If this piece touches all three sides of the triangle, then its complement has at least two disconnected regions (since it can't take up an entire side), so the pieces in those regions are at most pentagons by a similar analysis. If it does not touch all three sides of the triangle, then it is itself at most a pentagon.

If the polygons are triangles, then I can go through some casework on the edges to show that the triangles must be $30-60-90$ triangles, and from there derive a contradiction.

So the only remaining cases are those of quadrilaterals and pentagons. Can such dissections be shown impossible?

Interestingly, the answer is known to be yes for some squarefree multiples of $5$ like $180$; see this MathOverflow thread for a picture.

Answer 1

I have made some partial progress on the problem: The pentagon case is impossible! In fact, we can show the stronger statement that a triangle is not the union of any five strictly convex pentagons.

Suppose we had such an arrangement. Then we can create a graph on $8$ vertices as follows: we have a vertex for each pentagon, where we connect two pentagons with an edge if they share a positive-measure part of their borders. We also have three vertices positioned above each face of the triangle, connected to one another and to every pentagon whose border occupies a positive-measure part of the corresponding side of the triangle. Here is an image to illustrate the idea, though (by necessity) not all of the regions are pentagons.

Clearly, such a graph is planar. However, a planar graph on $n>2$ vertices has at most $3(n-2)$ edges, which can be seen by triangulating and using $V-E+F=2$. So this graph has at most $18$ edges, which means it has at most $36$ half-edges (which we can think of as ordered pairs of adjacent vertices).

Each vertex on the inside of the triangle has degree at least 5 (one for each side of the pentagon), so they contribute at least $25$ half-edges. However, a planar graph on $5$ vertices has at most $9$ edges, so at most $18$ of these half-edges are between two red vertices (to use the coloring in the diagram); at least $7$ must be between a red and a blue vertex.

Each of these red-blue edges (of which we now know there are at least $7$) contributes another half-edge (since we have only counted the red "side" of them), bringing our total to $32$. But then the three blue-to-blue edges (and thus six half-edges) takes us to $38$, yielding a contradiction.

This sort of analysis will not work on the quadrilateral case, however, as a triangle can be decomposed into five strictly convex quadrilaterals; the congruence assumption must be utilized somehow.

Answer 2

Well, the problem does not really say it has to be a Euclidean triangle ... .

On a sphere, draw a trirectangular triangle. Any one of its vertex angles, which we may think of as a north or south Pole, can be quintisected with an unmarked straightedge (matched to great circles on the sphere) and compasses, as a regular pentagon may be constructed on a sphere and its central angle may be used to quintisect a right angle. With the angle quintisection accomplished, the meridians are then drawn to the "equator" opposite the quintisected vertex.

The "cheat", of course, is that in spherical geometry you can draw multiple perpendiculars from a point to a suitably selected line/great circle. Not so in Euclidean geometry.