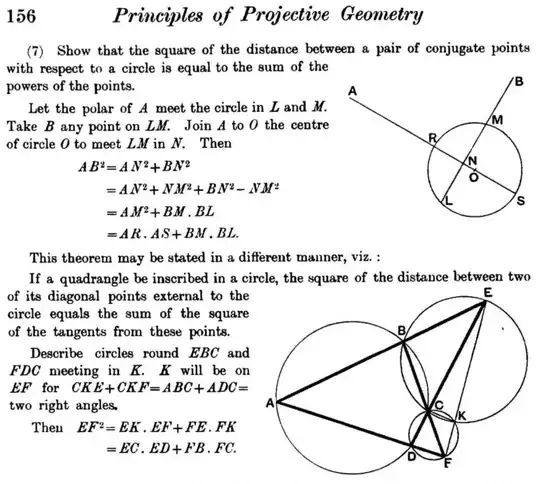
$4$ points in order $A,B,C,D$ lie on a circle with the extension of $AB$ meeting the extension of $DC$ at $E$ and that of $AD$ and $BC$ at $F$.

Question

$4$ points in order $A,B,C,D$ lie on a circle with the extension of $AB$ meeting the extension of $DC$ at $E$ and that of $AD$ and $BC$ at $F$. Let $EP$ and $FQ$ be tangents to this circle with points of tangency $P$ and $Q$ respectively. Suppose $EP = 60$,$FQ = 63$. Find $EF$.

What I Tried: Here's a picture :-

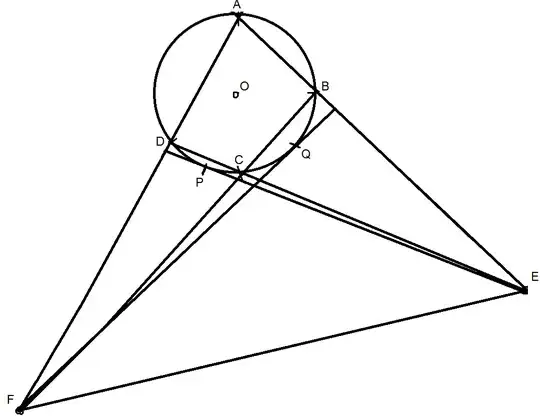
Used Power of a Point to get :- $$EA * EB = ED * EC = 3600$$ $$FA * FD = FB * FC = 3969$$ Yet this does not help to proceed and neither finds the value of $EF$ .

I thought of Pythagoras Theorem once. Join OP and OQ and let them be $x$ each . Then we can find $OE$ and $OF$ in terms of $x$ . Not sure if that helps in the problem though.

Can anyone help me? Thank You.

Answer 1

As I showed in this post, given a circle $\Gamma$ and two points $X,Y$ such that $Y$ lies on the polar of $X$ w.r.t. $\Gamma$, we have

$$XY^2=\text{Pow}_{\Gamma}(X)+\text{Pow}_{\Gamma}(Y)$$

Back to your case, it is well-known that $E$ lies on the polar of $F$ w.r.t. the circumcircle of $ABCD$ (recall, for example, how to prove Brokard's Theorem) and, hence, $$EF^2=60^2+63^2=7569\iff EF=87$$

Answer 2

Hatton's Projective Geometry, pg 156 gives two versions of a theorem:

[T]he square of the distance between a pair of conjugate points with respect to a circle is equal to the sum of the powers of the points.

and

If a quadrangle be inscribed in a circle, the square of the distance between two of its diagonal points external to the circle equals the sum of the square of the tangents from these points.

The second version uses your setup.

Here's a screen capture of the theorems and their proofs.

The proofs should be easy to follow, except for perhaps the last sentence. A more explicit version would be

$$ \begin{align} EF^2 &= (EK+KF)^2 \\ &= EK^2+2EK\cdot FK+FK^2 \\ &= EK(EK+KF)+(EK+FK)FK \\ &= EK\cdot EF + EF\cdot FK \\ &= EC\cdot ED + FB\cdot FC \text{ (using powers of $E,F$ wrt circles $CDF,BCE$)}\\ &= \text{sum of powers of $E$ and $F$ wrt original circle $ABCD$} \end{align} $$