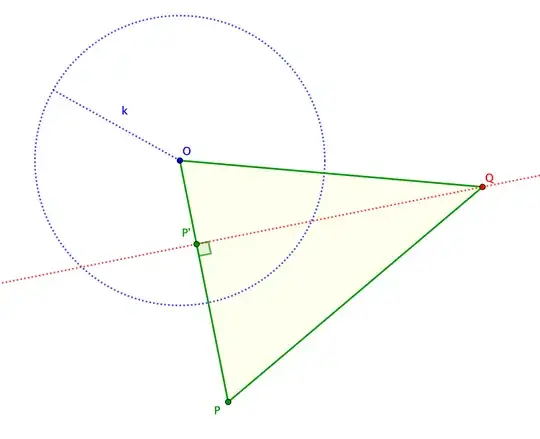
Reading a plane geometry book I found the following exercise:
Given a circle $K=(O,k)$ and a point $P$, the power of $P$ with respect to $K$ is the quantity $|OP|^2-k^2$. Let $P$ and $Q$ be conjugates with respect to $K$. Show that $|PQ|^2$ is the sum of the powers of $P$ and $Q$ with respect to $K$.
Note: Given a circle $K$ and two points $P$ and $Q$, we say they are conjugate points with respect to $K$ if the polar of each point passes through the other point.
I was thinking about using the pythagorean theorem and the definition of inverse point. However, I didn't get the desired result.