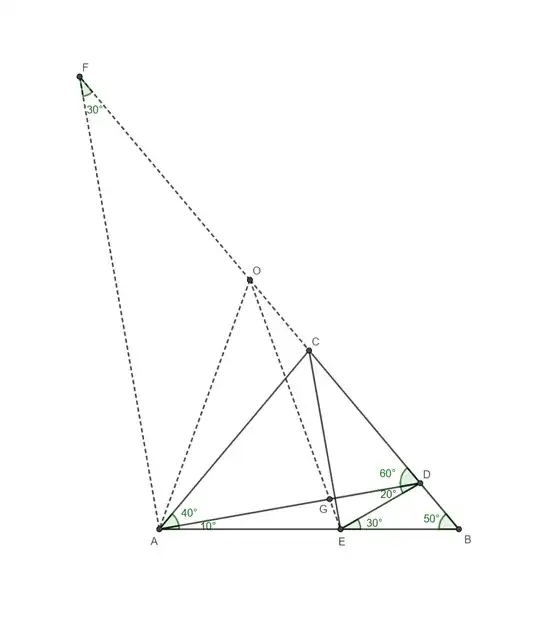
Here's the proof with sine rule. This will be the shortest solution, but it is inelegant, as is the case with all "World's Hardest Easy Geometry Problem" type problems. And as with all those questions, there will be a nice solution, (hopefully.) Consider the "simplified" diagram below.
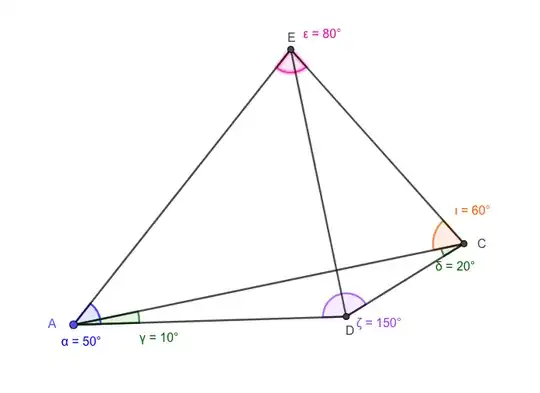
I messed up the naming so we are looking for $\theta = \angle EDC$.
In $\triangle CDE: \dfrac {EC}{\sin \theta} = \dfrac {DC}{\sin (180^\circ - 80^\circ - \theta)} = \dfrac {DC}{\sin (80^\circ + \theta)}$
In $\triangle ACE: \dfrac {EC}{\sin 40^\circ} = \dfrac {AC}{\sin 80^\circ}$
In $\triangle ACD: \dfrac {AC}{\sin 150^\circ} = \dfrac {DC}{\sin 10^\circ}$
Hence:
$$\frac {\sin (80^\circ + \theta)}{\sin \theta} = \frac {DC}{EC} = \frac {AC \sin 10^\circ}{\sin 150^\circ} \cdot \frac {\sin 80^\circ}{AC \sin 40^\circ} = \frac {\sin 10^\circ \sin 80^\circ}{\sin 150^\circ \sin 40^\circ}$$
$$\frac{\sin (80^\circ + \theta)}{\sin \theta} = \frac {\sin 80^\circ \cos \theta + \cos 80^\circ \sin \theta}{\sin \theta} = \sin 80^\circ \cot \theta + \cos 80^\circ$$
Thus we have:
\begin{align}\theta &= \cot^{-1} \left(\frac {\sin 10^\circ}{\sin 150^\circ \sin 40^\circ}-\cot 80^\circ\right)\\
& = \cot^{-1} \left(\frac {\sin 10^\circ}{\sin 30^\circ \sin 40^\circ}-\tan 10^\circ\right)\\
& = \cot^{-1} \left(\frac {2\sin 10^\circ}{4\sin10^\circ \cos 10^\circ \cos 20^\circ}-\frac{\sin 10^\circ}{\cos 10^\circ}\right)\\
& = \cot^{-1} \left(\frac {1}{2\cos 10^\circ \cos 20^\circ}-\frac{\sin 10^\circ \cos 20^\circ}{\cos 10^\circ \cos 20^\circ}\right)\\
& = \cot^{-1} \left(\frac {\sin 30^\circ - \sin 10^\circ \cos 20^\circ}{\cos 10^\circ \cos 20^\circ}\right)\\
& = \cot^{-1} \left(\frac {\cos 10^\circ \sin 20^\circ}{\cos 10^\circ \cos 20^\circ}\right)\\
& = \cot^{-1} \tan 20^\circ\\
& = 70^\circ
\end{align}
The last steps are only possible if we know in advance the solution is nice.
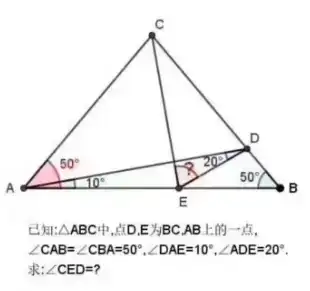 . The goal of the problem is to find the measure of $\angle DEC$ using the given angle measures provided. I've tried working on this to see what other angle measures I could deduce, and I'm including that here
. The goal of the problem is to find the measure of $\angle DEC$ using the given angle measures provided. I've tried working on this to see what other angle measures I could deduce, and I'm including that here 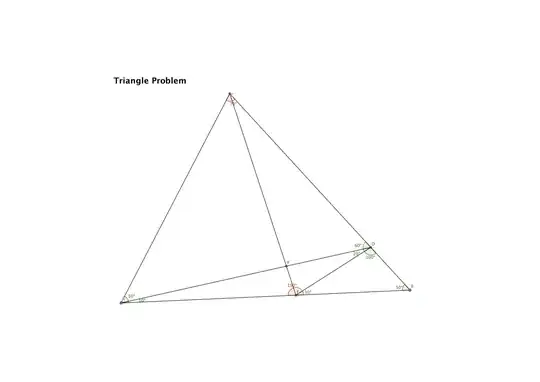 This is where I'm stuck. I've tried:
This is where I'm stuck. I've tried: