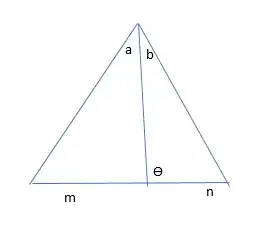
I was reading a textbook and found the following identity for the triangle given in the picture: $$(m+n)\cot(θ)= m\cot(a)-n\cot(b)$$ I tried to prove it using sine and cosine on the triangles but didn't get an expression that seemed to simplify. How should one prove this rule?
You can prove this rule using the sine law, which gives the following: $$\frac{n}{\sin b} = \frac{q}{\sin (b+\theta)},$$ $$\frac{m}{\sin a} = \frac{q}{\sin (\theta-a)},$$ where $q$ is the line between both triangles. If you now write both equations in terms of $q$, you get the following: $$n \frac{\sin (b+\theta)}{\sin b} = m \frac{\sin (\theta-a)}{\sin a}.$$ Now you can use $\sin (\alpha \pm \beta) = \sin \alpha \cos \beta \pm \cos \alpha \sin \beta$ to get: $$n \frac{\sin b \cos \theta + \cos b \sin \theta}{\sin b} = m \frac{\sin \theta \cos a - \cos \theta \sin a}{\sin a}.$$ Simplifying the expression, rearranging the terms and dividing by $\sin \theta$ you get the desired result: $$(m+n) \cot \theta = m \cot a - n \cot b.$$
