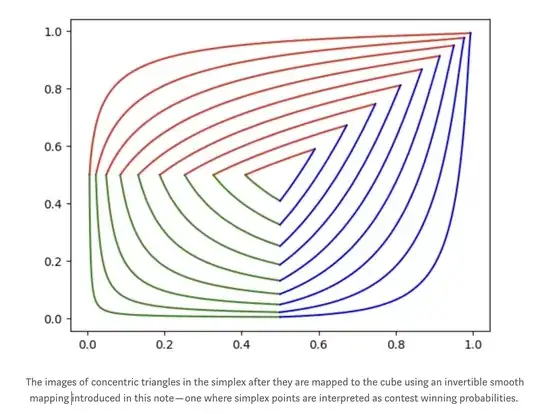
For a point $P=(x_1,...,x_n)$ in the unit cube $0 \le x_i \le 1$, define
$$s=x_1+\cdots +x_n, \ \ \ m=\max(x_1,...,x_n).$$
Then map $P$ to the point
$$f(P)=(x_1 \cdot \frac{m}{s},...,x_n \cdot \frac{m}{s}).$$
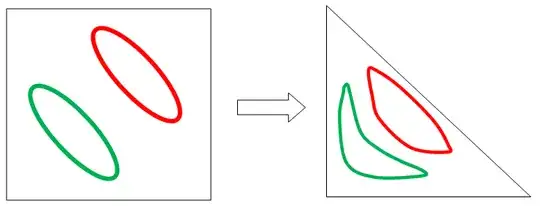
This maps the unit cube onto the simplex $x_i \ge 0, \ \sum x_i \le 1.$
This map works by contracing each ray from the origin to $P$ by the right amount so that it ends up inside or on the boundary of the simplex. A few examples in 3-d:
$F(P)=F((1/3,1/3,1/3))=(1/9,1/9/1/9).$ Here $F(P)$ is strictly inside the simplex. If one follows the ray from the origin through $P$ one will hit the remote corner $P'=(1,1,1)$ of the cube, for which $f(P')=(1/3,1/3,1/3),$ a point exactly on the boundary of the simplex.
Or look at $F(P)=F((1/2,1/3,1/4))=(3/13,2/13,3/26)$ inside the simplex, while if we rescale $P$ until its largest coordinate becomes $1$ to obtain $P'=(1,2/3,1/2)$ (so that $P'$ lies on the boundary of the unit cube) we find that $f(P')=(6/13,4/13,3/13)$, again a point exactly on the boundary since its coordinates sum to 1.
 http://tinypic.com?ref=30bcxzp
http://tinypic.com?ref=30bcxzp