Is there a homeomorphism between the $n$-dimensional cube to the $n$-dimensional simplex that doesn't create hard corners?

Question

Is there a homeomorphism between the $n$-dimensional cube to the $n$-dimensional simplex that doesn't create hard corners? This is related to a similar question found here. However, the mappings in response to that question create corners. Specifically, I've been playing with schemes where

1. Set a direction to squeeze the point $x\in[0,1]^n$, $v$
2. Project $x$ into the nullspace of $v$, $y = x - \frac{v^Tx}{v^Tv}v$
3. Draw a line between $x$ and $y$, $l(\alpha) = \alpha(y-x)+x$
4. $l(0)=x$, so we know it's in the hypercube. Find $$ \alpha_l = \arg\max\{\alpha\geq 0:l(\alpha)\in[0,1]^n\} $$ $$ \alpha_r = \arg\min\{\alpha\leq 0:l(\alpha)\in[0,1]^n\} $$ Basically, how far left and right we can travel and stay inside the cube
5. Define the squeeze factor $$ \alpha = \frac{\alpha_l}{\alpha_l-\alpha_r} $$ Basically, how far between the leftmost and rightmost points we are along the direction $v$.
6. Determine a new leftmost and rightmost point on the simplex, $$ z_l = l(\alpha_l) $$ $$ z_r = \frac{1-\sum x_i}{\sum (y_i-x_i)} $$ It turns out the left most point is the same for the cube and the simplex.
7. Use the squeeze factor to determine the new mapping for $x$ $$ w=\alpha(z_r-z_l)+z_l $$

Anyway, that was a little circuitous, but it works. It turns out if $v=(1,\dots,1)$, we get the first answer to the linked question above. If we set $v = x$, we get the second scheme.

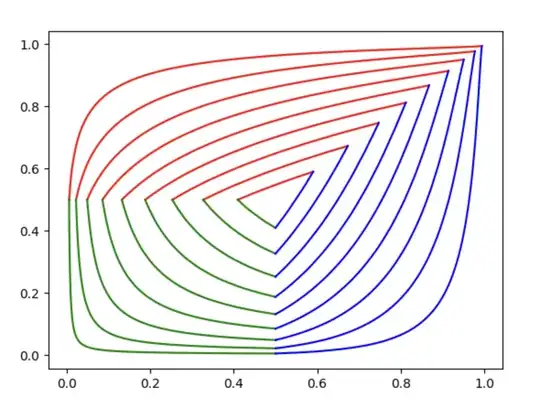
Alright, so what's the problem? This mapping makes something that kind of looks like a reentrant corner on smooth areas mapped to the simplex. For example, if we set $v=(1,\dots,1)$ and map a circle centered at $(0.5,0.5)$ of radius $0.25$ to the simplex, we go from 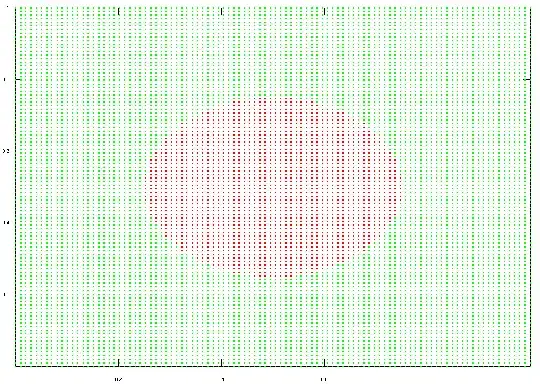to 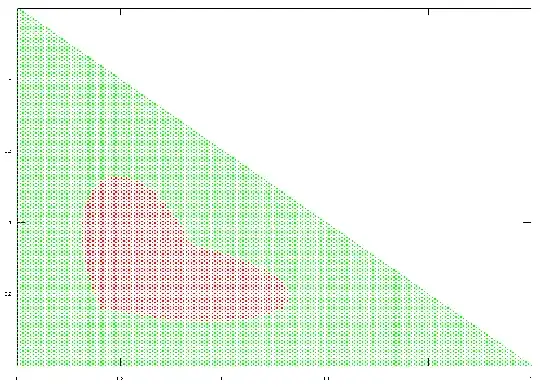Basically, we get a heart shaped object with these hard corners. I've tried a bunch of different schemes for choosing $v$ and I keep getting corners, which is undesirable. I really want something that's mapped smoothly to the simplex.

Anyway, is there a smooth map from the hypercube to the simplex where where something like a circle mapped from the hypercube to the simplex won't have these corners?

---

Edit 1

I think @Del has a good answer and here's what it looks like. Given a rectangular grid

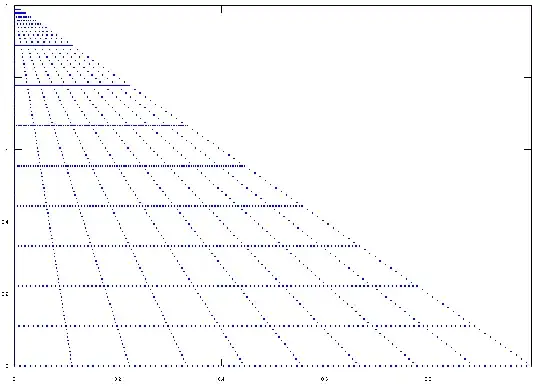
The scheme transforms this into

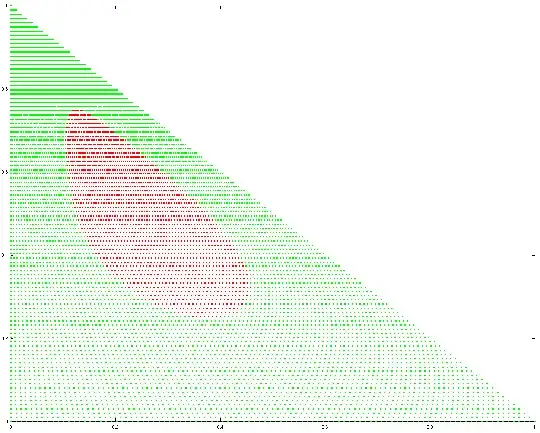
which shows how the grid is squished to fit into the simplex. It turns out this is smooth for the use case I described above. We can see this with the deformed circle

Anyway, thanks for the help!

Answer 1

I have one $C^\infty$ in the interiors: first of all the cube I'm considering is $C=(0,1)^n$, while the simplex $S$ is the interior of the convex hull of $\{0,e_1,\ldots,e_n\}$, where $\{e_i\}$ is the standard orthonormal basis of $\mathbb R^n$. If $O$ denotes the open positive orthant then $C=O\cap \{x:\|x\|_\infty< 1\}$ and $S=\{x:\|x\|_1< 1\}$.

The diffeomorphism is $f:C\to S$ defined by $$\left(f(x)\right)_i=x_i\prod_{i<j\leq n}(1-x_j)= x_i(1-x_n)\cdots (1-x_{i+1}).$$ For instance in $\mathbb R^3$ it's $$ \begin{pmatrix}x\\y\\z\end{pmatrix}\mapsto \begin{pmatrix} x'\\y'\\z'\end{pmatrix}=\begin{pmatrix}x(1-y)(1-z)\\y(1-z)\\z\end{pmatrix}.$$ You can check by backwards substitution that the inverse is $$ \begin{pmatrix}x'\\y'\\z'\end{pmatrix}\mapsto \begin{pmatrix} x\\y\\z\end{pmatrix}=\begin{pmatrix}\frac{x'}{1-y'-z'}\\\frac{y'}{1-z}\\z'\end{pmatrix}$$ or in general $$(f^{-1}(x'))_i=\frac{x'_i}{1-\sum\limits_{i<j\leq n}x'_j}.$$ It is obviously smooth. Let us check it sends $C$ to $S$ by induction on $n$. The case $n=2$: $$x_1(1-x_2)+x_2=(1-x_2)(x_1-1)+1\leq 1$$ and assuming the result true for $n-1$ $$\sum_{i=1}^n x_i\prod_{i<j\leq n}(1-x_j)=x_n+(1-x_n)\sum_{i=1}^{n-1}\prod_{i<j\leq n-1}(1-x_j)\leq x_n +(1-x_n)=1.$$ Moreover $f^{-1}$ sends $S$ to $C$: $$\frac{x'_i}{1-\sum_{i<j\leq n}x'_j}\leq \frac{1-\sum_{j\neq i}x'_j}{1-\sum_{i<j\leq n}x'_j}\leq 1.$$

What it essentially does is collapsing some faces into other lower dimensional ones (as suggested by Pedro Tamaroff in the comments) and interpolating sort of linearly in the middle.

Answer 2

See my answer to the duplicate question here.