0

Consider a convex quadrilateral with vertices at $a, b, c$ and $d$ and on each side draw a square lying outside the given quadrilateral, as in the picture below. Let $p, q, r$ and $s$ be the centers of those squares:

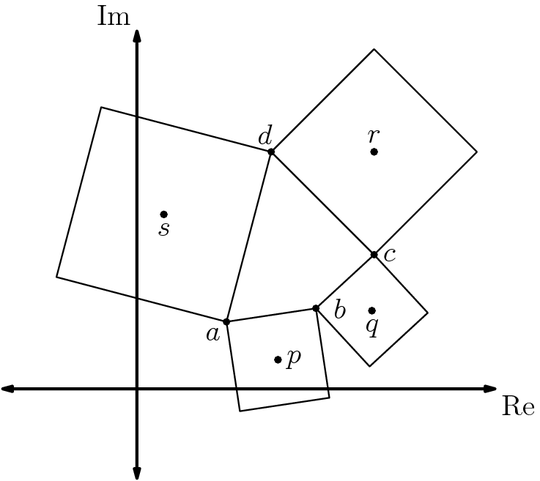
diagram

a) Find expressions for $p, q, r$ and $s$ in terms of $a, b, c$ and $d$.

b) Prove that the line segment between $p$ and $r$ is perpendicular and equal in length to the line segment between $q$ and $s$.

I managed to do part A, via finding a diagonal and then the midpoint. For part (b), I found a coord-bash algebraic solution, via assigning a lot of variables. However, is there a geometric solution?

Martin Sleziak
  • 56,060
  • https://mathworld.wolfram.com/vanAubelsTheorem.html – Cheong Sik Feng Jun 13 '20 at 06:45
  • what did you try so far? –  Jun 13 '20 at 06:46
  • You should include your solution to part (a), as part (b) follows from it. This will help people avoid wasting time duplicating your effort or explaining what you already know. (And here's a hint: calculate $(p-r)/(q-s)$.) – Blue Jun 13 '20 at 06:51
  • For (a) I first did the case for a and b, which i did by finding the square's diagonal via translating b to the origin, then multiplying a by sqrt(2)e^(pi/4)i, then translating it back. Then I generalized. –  Jun 13 '20 at 07:23
  • Oh yeah I just realized it's Van Aubel's theorem. –  Jun 13 '20 at 07:43

1 Answers1

2

We can start off by translating $a$ to the origin using rotations and the fact that we can scale the distance of b and a, we come up with $p=a +\frac{\sqrt{2}}{2} e^{\pi*i/4}(b-a)$ Since $\frac{\sqrt{2}}{2}e^{\pi*i/4} = \frac{1}{2} - i\frac{1}{2}$, we can rewrite the equation to get $p = \frac{1}{2}$ $(a(1+i)$ $+$ $b(1-i))$ Simplifying this to get $p = \frac{a + b + ia - ib}{2}$, we can rewrite this in a more appealing way: $p = \frac{a + b}{2} + \frac{i(a - b)}{2}$. We can use the same strategy of translating to the origin and rotating segments for all other complex points in order to define the complex numbers q, r, s. $q = \frac{b + c}{2} + \frac{i(b - c)}{2}$ $r = \frac{c + d}{2} + \frac{i(c - d)}{2}$ $s = \frac{d + a}{2} + \frac{i(d - a)}{2}$ (In order to get these, I used the fact that we had to translate to the origin and that $p$ is a 45 degree rotation from $b$, $q$ is a 45 degree rotation from $c$, r is a 45 degree rotation from $d$ and $s$ a rotation from $a$.) I also have just given a diagram for p(not sure if its correct) and I saw on the message board as long as I describe the other equation similarities(45 degree rotation) I can just leave it at that.

B: We want to prove that the line segment between $p$ and $r$ is perpendicular and equal in length to the line segment between $q$ and $s$. Translate where the two lines meet to the origin, then rotating one of the lines to get the other gives us $e^{\pi/2}(r-p)=s-q$. If $e^{\pi/2}(r-p)=s-q$, then $|r-p|=|s-q|$. The lines are perpendicular if $e^{\pi/2}(r-p)=s-q$ is true. Using values we got in a, we can see that $e^{\pi/2}(r-p)=s-q$, or $i(r-p)=s-q$ is made into $i\left(\frac{d-di+c-ci}{2}-\frac{b-bi+a-ai}{2}\right)=\frac{a-ai+d-di}{2}-\frac{c-ci+b-bi}{2}$. This gives us: $2di+2c=2a+2bi$, or $di+c=a+bi$

Peyton Hecht
  • 31
  • Yes, this is the complex-bash solution I was talking about. But is it possible to solve this problem geometrically? –  Nov 20 '22 at 22:27