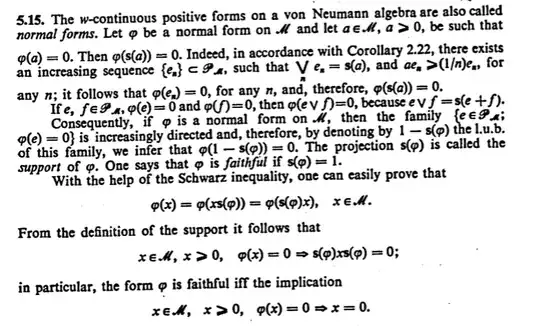The equivalence relation defined by normal form on Von Neumann algebra, its support and the it's representation .

Question

Let M be a von Neumann algebra and $\varphi$ a positve normal form on M.

$N = \lbrace x\in M | \varphi(x^*x)=0\rbrace $ . We denote $M_{\varphi} := M/N$ as the pre-Hilbert space defined by the inner product: $\langle a_{\varphi},b_{\varphi}\rangle = \varphi(b^*a)$, when $a_{\varphi}$ the equivalence class of $a\in M$.

We also denote $s :=s(\varphi)$ , the support of $\varphi$.

Q : I would like to know if $(sa)_{\varphi} = a_{\varphi}$ as equivalence classes.

I do know how to prove that $(as)_{\varphi} = a_{\varphi}$ since

$\varphi((as)^*as) = \varphi(s^*a^*as) = \varphi(sa^*as) = \varphi(a^*a) $ from the definition of the support. but if I am trying to do the same with $(sa)_\varphi$, I have: $\varphi((sa)^*sa) = \varphi(a^*sa)$ which I dont know what to do with.

If I am wrong and $(sa)_{\varphi} \neq a_{\varphi}$ then I have another question about the representation defined by $\varphi$ which we denote as $ \pi :=\pi_{\varphi} \colon M \to \pi_\varphi(M)$.

Q: is $\pi|_{M_s} \colon M_s \to \pi(M)$ surjective?(when $M_s = sMs$).

If $(sa)_\varphi = a_\varphi $ then the proof is immediate since $\langle \pi(sxs)a_\varphi,a_\varphi\rangle = \langle\pi(s)\pi(x)\pi(s)a_\varphi,a_\varphi \rangle = \langle \pi(x)\pi(s)a_\varphi,\pi(s)a_\varphi \rangle = \langle \pi(x)(sa)_\varphi,(sa)_\varphi \rangle = \langle \pi(x)a_\varphi,a_\varphi \rangle$

and we can conclude that $\pi(sxs) = \pi(x)$ and we have that $\pi|_{M_s}$ is surjective.

For the definition of the support of normal form:

Stratila, Serban; Zsidó, Lászlo, Lectures on von Neumann algebras. (Lectii de algebre von Neumann.), Bucuresti: Editura Academiei Republicii Socialiste Romania. 409 p. Lei 34.00 (1975). ZBL0324.46068.:

Answer 1

Your concern in the first question is not true, let $M=M_2(\Bbb C)$ and $\varphi(a) = a_{11}$ so that $s=|e_1\rangle\langle e_1|$ is the projection onto the first component. Now let $x= |e_2\rangle\langle e_1|$, then: $$\|[x]-[sx]\|^2= \varphi(((1-s)x)^*(1-s)x)) =\varphi(x^*(1-s)x)=\varphi(|e_1\rangle\langle e_2|e_2\rangle\langle e_2|e_2\rangle\langle e_1|)=\varphi(|e_1\rangle\langle e_1|)=1$$

Then your second question also cannot be true. $\pi(s)$ must be a projection, but it cannot be the identity so it admits a kernel in $\overline{M_\varphi}$. Since the above example is finite dimensional you have that $M_\varphi$ is already complete, so there must be some $x\in M$, $[x]\neq0$ but $[sx]=0$. So $[x]$ cannot be in the image of any $\pi(sys)$, but $\pi(x)[1]=[x]$, implying that $\pi(x)$ cannot be of the form $\pi(sys)$ for any $y\in M$.