The projective space $\Bbb RP^{2n}$ cannot be the total space of a nontrivial covering map

Question

Why is the projective space $\Bbb RP^{2n}$ not the total space of a nontrivial covering map? I've heard this in class but I can't see why it holds.

Answer 1

You've already worked out the answer in the comments, but just so that there is an official answer I will write it down.

Recall that the Euler characteristic is multiplicative for covering spaces, specifically if $E \to B$ is a covering space with $n$-sheets where $B$ is of finite type (by which I mean homology is finitely-generated in all degrees and non-zero in finitely many degrees so that the Euler characteristic is defined) then $\chi(E) = n\cdot \chi(B)$.

Note that $\chi(\mathbb{RP}^{2n}) = 1$. If $\mathbb{RP}^{2n} \to B$ is a covering space then by compactness it has finite fibres (say of size $n$) and $B$ is compact and hence of finite type, therefore

$$ 1 = n\cdot \chi(B).$$

The only possibility is that $n = 1$ and it is a trivial covering.

---

It's worth noting that $\mathbb{RP}^{2n+1}$ is the total space of non-trivial coverings, as it covers Lens spaces. See for example Covering $\Bbb RP^\text{odd}\longrightarrow X$, what can be said about $X$?

Answer 2

The question has been posted for a long time, but I have some doubts about the answer and comments above, i.e.

for a covering map $\pi\colon \mathbb{R}P^{2n}\to B$, can we ensure that $B$ has a CW complex structure?

And I decide to write another answer.

To prove the initial question, denote $X:=\mathbb{R}P^{2n}$, we know that any map (continuous) $f\colon X\to X$ must have a fixed point by applying the Lefshetz fixed point theorem.

Let $b\in B$, and $x,y\in X$ be two lifts of $b$. Consider the following diagram

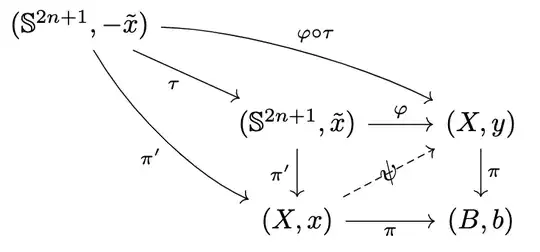
where $\pi'$ is the $2:1$ covering of $X$, and $\tau\colon \mathbb{S}^{2n+1}\to\mathbb{S}^{2n+1}$ is the antipodal map. Since $\mathbb{S}^{2n+1}$ is path connected and simply connected, there exists a unique map $\varphi\colon (\mathbb{S}^{2n+1},\tilde{x})\to(X,y)$ lifting $\pi\circ\pi'$. Therefore the diagram is commutative with the solid arrows. Thus $\varphi\circ \eta$ lifts $\pi\circ\pi'$, so we have $\varphi\circ\eta=\varphi$ by the uniqueness. Therefore $\varphi\colon (\mathbb{S}^{2n+1},\tilde{x})\to(X,y)$ factors through $\pi'$, i.e. there exists a map $\psi\colon (X,x)\to (X,y)$ such that the whole diagram commutes. By the argument above, the map $\psi$ must have a fixed point and therefore $\psi=\text{id}_X$. So we have $x=y$ and the covering $\pi\colon X\to B$ is trivial.