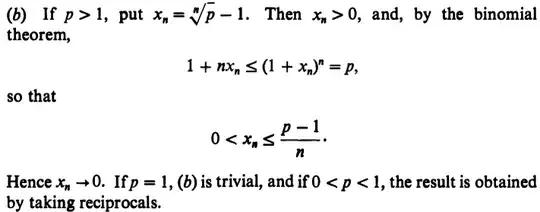6

The question is in the title. I will present the argument that I have for this.

Proof Attempt:

Let $a = 1$. Then, $a^{\frac{1}{n}} = 1$ for all $n \in \mathbb{N}$ so the limit is clearly equal to 1.

Let $a > 1$. Define $x_n = a^{\frac{1}{n}} - 1$. Then, we have:

$$a = (1+x_n)^n$$

I claim that $x_n > 0$ for all $n \in \mathbb{N}$. To show that this is true, suppose that $x_n \leq 0$. Then, $a^{\frac{1}{n}} < 1$ and that implies that $a \leq 1$. This is false under the given hypothesis that $a > 1$.

Now, we use Bernoulli's inequality and deduce that:

$$a = (1+x_n)^n \geq 1+nx_n \geq 1$$

$$\frac{a-1}{n} \geq x_n \geq 0$$

By the Squeeze Theorem, it follows that $x_n \to 0$ as $n \to \infty$. That is, $a^{\frac{1}{n}} \to 1$ as $n \to \infty$.

Suppose that $0 < a < 1$. Then:

$$b = \frac{1}{a} > 1$$

Clearly, the sequence defined by $x_n = b^{\frac{1}{n}}$ converges to 1. So:

$$\lim_{n \to \infty} b^{\frac{1}{n}} = 1$$

$$\lim_{n \to \infty} \frac{1}{b^{\frac{1}{n}}} = \frac{1}{\lim_{n \to \infty} b^{\frac{1}{n}}} = \lim_{n \to \infty} a^{\frac{1}{n}} = 1$$

That proves the desired result.

Is the proof above correct? If it isn't, why? How can I fix it?

Edit:

Since one individual has voted for this question to be closed, I want to explain why it's not a duplicate and the suggestion that it should be closed makes no sense.

This question requires a solution to be verified. Namely, my solution to the given problem is what needs to be verified. It needs to be criticized and holes need to be pointed out so that I may fix the proof. That's actually explicitly what I've asked in the last line of the original question.

Since I'm self-studying mathematics, it stands to reason that I may believe I have a proof but, in reality, do not have one. If someone can point out the mistake in my argument and if I can fix it without having to refer to another person's proof, then that would be more fruitful.

Let $a > 1$ and $x > 0$. Prove that $a^x > 1$

Please refer to the above link for another question I asked, where I believed that I had a proof of the result and several individuals chipped in to help me fix it. The mistake with respect to my proof was explicitly pointed out to me and that ended up being very useful. The question that was linked, while containing useful and insightful information that I would be interested in AFTER I proved the result, does not answer the question as I had asked it.

Mousedorff
  • 6,428
  • 4
    Couldn't you simply say that as $n$ approaches $\infty$ ,$\frac{1}{n}$ approaches $0$, so $a^{\frac{1}{n}}$ approaches 1? – A-Level Student Jun 09 '20 at 10:43
  • 4
    It looks fine to me. – José Carlos Santos Jun 09 '20 at 10:45
  • Your proof looks fine, but as A-level Student suggested, consider $a^{1/n}$ as exponential function, which is continuous. This is much easier. – mag Jun 09 '20 at 10:47
  • 2
    I can't use the fact that the exponential function is continuous because we haven't defined continuity for exponentials. Essentially, this is a build up to the definition of $a^x$ where $x \in \mathbb{R}$ – Mousedorff Jun 09 '20 at 10:54
  • @JoséCarlosSantos Thank you so much – Mousedorff Jun 09 '20 at 10:54
  • I would write the last line as $$ \lim_{n \to \infty} a^{\frac{1}{n}} = \lim_{n \to \infty} \frac{1}{b^{\frac{1}{n}}} = \frac{1}{\lim_{n \to \infty} b^{\frac{1}{n}}} = 1.$$ – Gary Jun 09 '20 at 12:28
  • 1
    Ohhh okay that makes more sense. I guess that's just to make things more clear, right? Thanks so much for the feedback. – Mousedorff Jun 09 '20 at 12:32
  • 2
    Previously asked: https://math.stackexchange.com/q/1867269/321264. – StubbornAtom Jun 09 '20 at 14:26
  • 1
    That isn't really the point. The point was to have my own proof/thought process verified as being correct. Thank you for the link, I'll have a look at it now that I'm sure my approach was correct. – Mousedorff Jun 09 '20 at 14:27
  • 1
    Thanks for the +1. If that was site policy, though, my questions would've very well been closed earlier. As it stands, most of them have remained up and have gotten many upvotes (i suppose this is because of the effort I put into writing my proofs/thoughts). The trouble with looking through the argument provided by another is that it doesn't exactly point to the flaw in my own proof and it also gives me the solution to the problem, something that I only want to have access to once i have been shown that my thoughts were either correct or completely wrong. – Mousedorff Jun 10 '20 at 07:54
  • 1
    For example, if i have successfully proved a result in my own way and someone else proposes another proof, that can be extremely enlightening. I should also point out that i'm self-studying math at the moment and i feel that it's imperative that my proofs be checked by those who are more mathematically mature than I am. – Mousedorff Jun 10 '20 at 07:55
  • Does this answer your question? Use $\delta-\epsilon$ to show that $\lim_{n\to\infty} a^{\frac{1}{n}} = 1$? – nmasanta Jun 10 '20 at 14:35
  • If you took the time to look above, then you'd see that Jose has already verified my proof. Regardless, it doesn't answer my question. StubbornAtom posted the exact same link. – Mousedorff Jun 10 '20 at 14:40
  • The question was for my proof to be verified to be correct or incorrect, not to provide another proof. I'd be fine with an alternative proof provided or a link given once my argument were verified to hold or not hold. So, it doesn't actually answer my question. Don't get me wrong, I've read through it and it's great. It's just not something I was initially looking for. – Mousedorff Jun 10 '20 at 16:11
  • +1.Yes correct. Why would you think that something is wrong with it? – Koro Jun 11 '20 at 07:13
  • I was initially skeptical because I thought that I would have to use an $\epsilon-\delta$ argument in order to prove this limit. So, I wasn't particularly sure that my own line of reasoning worked or not. I've kind of become super paranoid about whether my arguments are correct or not for these problems haha (not quite sure if that's justified) – Mousedorff Jun 11 '20 at 07:18

1 Answers1

2

I was initially skeptical because I thought that I would have to use an − argument in order to prove this limit.

No, a formal proof does not mean one has to use $\epsilon$-$\delta$.

And yes, I verify that your proof is correct.

Comments:

In the last step:

$$\lim_{n \to \infty} \frac{1}{b^{\frac{1}{n}}} = \frac{1}{\lim_{n \to \infty} b^{\frac{1}{n}}} = \lim_{n \to \infty} a^{\frac{1}{n}} = 1$$

the middle term $\frac{1}{\lim_{n \to \infty} b^{\frac{1}{n}}}$ is unnecessary.

Your proof is actually the same as that of the same statement in Rudin's Principal Mathematical Analysis (3rd edition, page 58). Rudin's presentation is more concise.

enter image description here