0

In one of my homework problems, I need to deduce that $\text{A} \vee \neg{\text{A}}$ without a premise.

The lecturer mentioned that students should "combine" answers for the previous two problems with some editing.

The previous two problems were to prove $\neg\left(\text{A} \vee \neg{\text{A}}\right) \vdash \neg\text{A}$ and $\neg\left(\text{A} \vee \neg{\text{A}}\right) \vdash \text{A}$.

This is what I did for both:

enter image description here

enter image description here

Also, for these problems, the lecturer gave a derivation format with a certain number of lines like this: enter image description here

For combining these two, I was thinking I need an $\vee$-elimination to somehow get $\text{A} \vee \neg\text{A}$. When I combine these two for the original problem, I get this:

enter image description here

But I feel like I would need to more lines stating $\text{A} \vee \neg\text{A}$ after lines 5 and 9.

Mauro ALLEGRANZA
  • 99,247
Ansar Al
  • 391

1 Answers1

2

The rules of negation elimination and negation introduction in your proof system requires the derivation of two contradictions within the context of the assumption.    Now, the assumption and its own contradiction would suffice, but it is only necessary to derive any two contradictory statements.

$$\begin{array}{|l}~~~~\begin{array}{|l} \neg P\\\hline~~\vdots\\~~ Q\\~~\vdots\\\neg Q\end{array}\\~~P\end{array}\qquad\begin{array}{|l}~~~~\begin{array}{|l} ~~ P\\\hline~~\vdots\\~~ Q\\~~\vdots\\\neg Q\end{array}\\\neg P\end{array}$$

So your proof is quite okay as it stands.

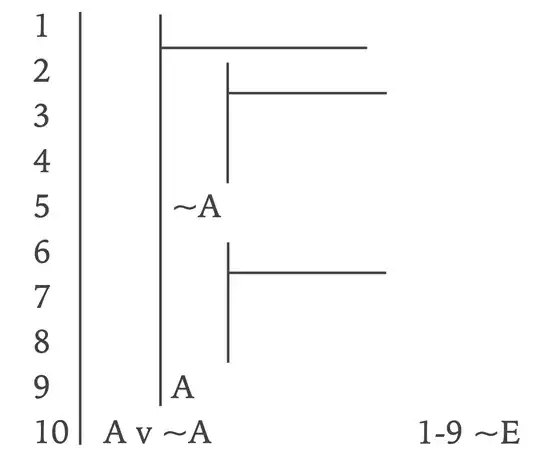
$$\begin{array}{|l}~~~~\begin{array}{|l}~~1.~\neg (A\vee\neg A)\\\hline~~\begin{array}{|l}~~2.~A\\\hline~~3.~ A\vee\neg A\hspace{10ex}{\vee}\mathrm I~2\\~~4.~\neg(A\vee\neg A)\hspace{7ex}\mathrm R~1\end{array}\\~~5.~\neg A\hspace{17ex}{\neg}\mathsf I~2{-}4\\~~\begin{array}{|l}~~6.~\neg A\\\hline~~7.~ A\vee\neg A\hspace{10ex}{\vee}\mathrm I~6\\~~8.~\neg(A\vee\neg A)\hspace{7ex}\mathrm R~1\end{array}\\~~9.~~~ A\hspace{17ex}{\neg}\mathsf E~6{-}8\end{array}\\10.~A\vee\neg A\hspace{15.5ex}{\neg}\mathsf E~1{-}9\end{array}$$

Now, since that is the skeleton you were required to fill, you have done what was asked.

Of course, there are other skeletons and the standard proof prunes things down just a bit.

$$\begin{array}{|l}~~~~\begin{array}{|l}~~1.~\neg (A\vee\neg A)\\\hline~~\begin{array}{|l}~~2.~A\\\hline~~3.~ A\vee\neg A\hspace{10ex}{\vee}\mathrm I~2\\~~4.~\neg(A\vee\neg A)\hspace{7ex}\mathrm R~1\end{array}\\~~5.~\neg A\hspace{17ex}{\neg}\mathsf I~2{-}4\\~~6.~ A\vee\neg A\hspace{12ex}{\vee}\mathrm I~5\end{array}\\~~7.~A\vee\neg A\hspace{15.5ex}{\neg}\mathsf E~1{-}6\end{array}$$

Graham Kemp
  • 133,231