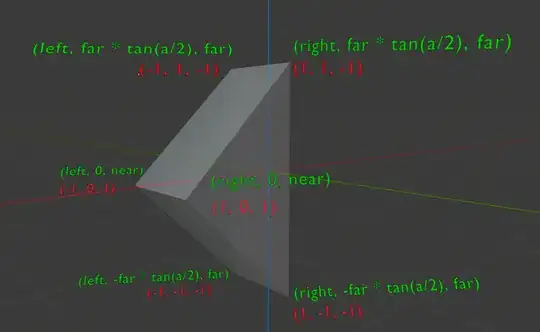
I have a problem finding a linear transformation for the following case:
I want the green coordinates beeing transformed into the red coordinates by a 4x4 matrix with the following specification:
Input is the vector $\vec{v}_{in} = \begin{pmatrix}v_{i,x}\\v_{i,y}\\v_{i,z}\end{pmatrix}$ which is transformed into the output vector $\vec{v}_{out}$ by the 4x4-matrix I am looking for $A$ by:
$A \begin{pmatrix}v_{i,x}\\v_{i,y}\\v_{i,z}\\1\end{pmatrix} = \vec{v}_{temp} = \begin{pmatrix}v_{t,x}\\v_{t,y}\\v_{t,z}\\v_{t,w}\end{pmatrix}$
$\vec{v}_{out} = \begin{pmatrix}v_{o,x}\\v_{o,y}\\v_{o,z}\end{pmatrix} = \begin{pmatrix}\frac{v_{t,x}}{v_{t,w}}\\\frac{v_{t,y}}{v_{t,w}}\\\frac{v_{t,z}}{v_{t,w}}\end{pmatrix}$
The question is: What is this matrix $A$?
Background: I want a custom projection matrix, which is perspective in one dimension and orthgraphic in the other dimension. I also tried to calculate it, but I always get stuck in the fact, that $v_{o,x}$ does not depend on $v_{i,z}$ but $v_{o,y}$ does depend on $v_{i,z}$.