Projection matrix which is orthographic in one dimension and perspective in the other

Question

I need a custom projection matrix, which is orthographic in one dimension and perspective in the other. That means I need to map the vertices of a trapezoidal prism in real world coordinate system to the vertices of a unit cube.
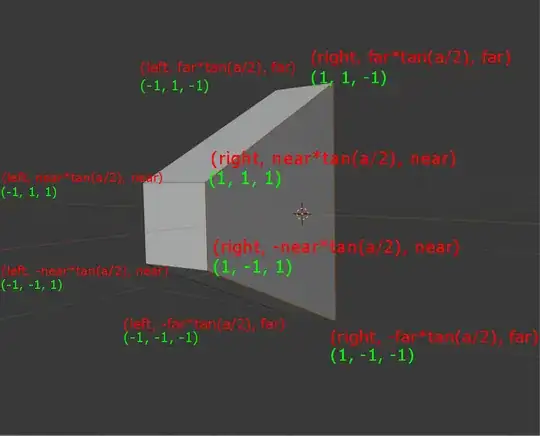
I tried to visualize it in the following image:

The red coordinates (in real world coordinate system) must be mapped to the green coordinates (unit cube).

What does the projection matrix look like?

After a bit of thought I think that it might be equally helpfull to find a transformation which compresses a cube on one side and forms the cube into a trapezoidal prism with a square base.
Is there a known transformation matrix for this?
In pursuit of this train of thought I found this image with a transformation of a square into a trapez on this site.

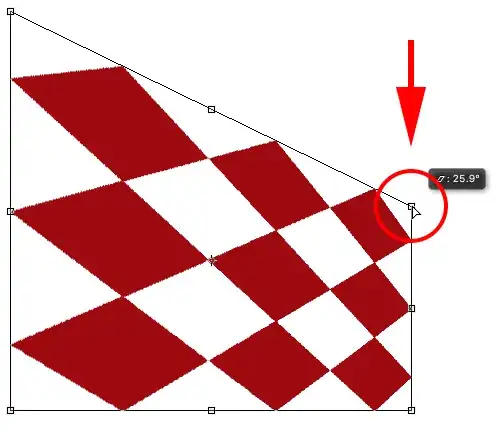
I know that this is only in 2D, but maybe it would be helpfull to now this transformation and expand it to my case with 3 dimensions.

What have I done already: My first try was to use a triangle prism as view frustum, so I asked this question. But when I used the projection matrix from the answer I got strange results (it seems like the projection was not perspective at all - neither in $x$ direction nor in $y$ direction). I thought, that this might be because I had no near clipping plane.
So I tried to use the equation given and tried to calculate the matrix by myself:

$$ \begin{align} A&= \begin{pmatrix}1&1&1&-1\\ \:1&1&-1&-1\\ \:1&-1&-1&1\\ \:1&1&1&1\end{pmatrix} \begin{pmatrix}r&r&r&l\\ \:n\cdot \:t&f\cdot \:t&-f\cdot \:t&-n\cdot \:t\\ \:n&f&f&n\\ \:1&1&1&1\end{pmatrix}^{-1} \\ A &= \begin{pmatrix}1&1&1&-1\\ \:1&1&-1&-1\\ \:1&-1&-1&1\\ \:1&1&1&1\end{pmatrix} \begin{pmatrix}-\frac{1}{-r+l}&0&\frac{1}{-f+n}&-\frac{lf-nr}{\left(-f+n\right)\left(-r+l\right)}\\ \frac{n}{f\left(-r+l\right)}&\frac{1}{2tf}&\frac{-f-n}{2f\left(-f+n\right)}&\frac{n\left(-nr+lf\right)}{f\left(-f+n\right)\left(-r+l\right)}\\ -\frac{n}{f\left(-r+l\right)}&-\frac{1}{2tf}&\frac{1}{2f}&\frac{nr}{f\left(-r+l\right)}\\ \frac{1}{-r+l}&0&0&-\frac{r}{-r+l}\end{pmatrix}\\ A&= \begin{pmatrix}-\frac{2}{-r+l}&0&0&\frac{l+r}{-r+l}\\ \frac{-2f+2n}{f\left(-r+l\right)}&\frac{1}{ft}&-\frac{1}{f}&\frac{lf-2nr+rf}{f\left(-r+l\right)}\\ 0&0&\frac{2}{-f+n}&-\frac{f+n}{-f+n}\\ 0&0&0&1\end{pmatrix} \end{align} $$

This seems correct for the four vertices with which I constructed my matrix, e.g. $A\begin{pmatrix}r\\nt\\n\end{pmatrix} = \begin{pmatrix}1\\1\\1\end{pmatrix}$

But when I try to transform the other four vertices I get wrong results:

$$ A\begin{pmatrix}l\\ft\\f\end{pmatrix} = \begin{pmatrix}-1\\\pmb{0.5}\\-1\end{pmatrix} should\;be \begin{pmatrix}-1\\1\\-1\end{pmatrix}\\ A\begin{pmatrix}l\\nt\\n\end{pmatrix} = \begin{pmatrix}-1\\\pmb{0.5}\\1\end{pmatrix} should\;be \begin{pmatrix}-1\\1\\1\end{pmatrix}\\ A\begin{pmatrix}r\\-nt\\n\end{pmatrix} = \begin{pmatrix}1\\\pmb{-0.5}\\1\end{pmatrix} should\;be \begin{pmatrix}1\\-1\\1\end{pmatrix}\\ A\begin{pmatrix}l\\-ft\\f\end{pmatrix} = \begin{pmatrix}-1\\\pmb{-1.5}\\-1\end{pmatrix} should\;be \begin{pmatrix}-1\\-1\\-1\end{pmatrix} $$

This is the point, where I don't know how to proceed to get it right. What is wrong with my calculations (I think I double-checked everything)?
I noticed that only the $y$ component is wrong, but I don't know how this could lead me into the right direction...

Answer 1

TL;DR There is no such matrix.

That’s not to say that you couldn’t construct a transformation that maps the two volumes as you’d like, but there’s no projective transformation of space that can accomplish this, so the transformation can’t be implemented as multiplication by a constant $4\times4$ homogeneous matrix.

We can see that this is so because projective transformations map lines to lines and preserve incidence relationships. The extensions of the edges of the destination cube parallel to the $x$-axis all intersect at a single point (at infinity), so the extensions of the corresponding edges of any preimage of the cube must also have a common intersection point.k This is clearly not the case for your trapezoidal prism.

A fairly straightforward algebraic calculation also shows that it’s impossible to construct such a matrix. Observe that the bounding planes of the frustrum can be recovered from the projection matrix $P$. We can represent planes by homogeneous vectors $\mathbf p$, so that the equation of the plane is $\mathbf\pi^T\mathbf x=0$. If we have $\mathbf x'=P\mathbf x$, then $\mathbf\pi^T(P^{-1}\mathbf x') = (P^{-T}\mathbf \pi)^T\mathbf x' = 0$, so the plane $\mathbb\pi$ is mapped to $P^{-T}\mathbf\pi$. In other words, $P^T$ maps planes in the destination space to planes in the source space. Moreover, that source plane is a linear combination of the rows of $P$ (which I’ll denote by $\mathbf P_i$) with coefficients given by the components of the destination plane vector.

Now, the near, far, left, right, top and bottom faces of the destination cube are, respectively, on the planes $(0,0,1,-1)$, $(0,0,1,1)$, $(1,0,0,1)$, $(1,0,0,-1)$, $(0,1,0,-1)$ and $(0,1,0,1)$. So, the corresponding source planes are just the sums and differences of the first three rows of $P$ and its last row. For example, the near plane is $\mathbf P_3-\mathbf P_4$. The actual near plane of the source prism is $(0,0,1,-n)$, so we now have the constraint $\mathbf P_3-\mathbf P_4=c_1(0,0,1,-n)$ for some nonzero $c_1$.† Similarly, identifying the two far planes produces $\mathbf P_3+\mathbf P_4=c_2(0,0,1,-f)$. Subtracting the first from the second yields the expression $\frac12(0,0,c_1-c_2,c_1n-c_2f)$ for the last row $\mathbf P_4$. Doing the same for the other two face pairs produces two other expressions for $\mathbf P_4$. They must all be equal, so we end up with a system of linear equations in the unknown coefficients $c_i$. If you go through the computation, you’ll find that this system has only the trivial solution, but even before you’ve gotten that far, you’ll find that we must have $\mathbf P_4=0$, which doesn’t make for a healthy projection matrix.

---

† Since we’re working with homogeneous vectors and matrices, we have to be careful about using strict equality in these constraints. Since $\mathbf v$ and $k\mathbf v$ (for $k\ne0$) represent the same point/plane, we have to introduce unknown multipliers in the equations that represent point or plane pair constraints. Strict equality, which is what was used to develop the solution to your related question, restricts us to affine transformations, which obviously won’t work here since the images of parallel lines aren’t parallel. You could try to adapt the 2-D method described in this answer, but since the transformation that you’re looking for isn’t projective, that will fail, too.