Consider an ellipse and a circle inside it. They have the same center. Let $P$ be a moving point on the ellipse. Through $P$, draw the two tangents to the circle, which meet the ellipse at $A,B$. Again, through $A,B$ respectively, draw the tangents to the circle, which meets each other at $Q$. What's the locus of $Q$?
By software graphing, it seems to be an ellipse too. But how to prove this without much computation? It's better to explain by projective geometry.
This is an algebraic proof using complex numbers. It is not simple but not that horrible. One corollary of this proof is coordinates of $P$ and $Q$ are related by different scaling in $x$- and $y$- direction $(*2')$. I think this could be a key for any geometric proof of this interesting problem.
Choose a coordinate system so that the circle/ellipse are centered at origin, the circle has unit radius and the semi-major axis of the ellipse is the $x$- axis. Let $\alpha, \beta$ be the semi-major and semi-minor axes of the ellipse. We will assume $\alpha > \beta > 1$ so that the ellipse lies completely outside the circle.
Identify points with complex numbers. We will use upper case letter to denote a point and same lower case letter to denote corresponding complex number.
Let $Z = (x,y)$ be any point outside the unit circle. $z = x + iy$ and $Z$ lies on the ellipse when and only when $$\begin{align}\frac{x^2}{\alpha^2} + \frac{y^2}{\beta^2} = 1 &\iff \frac{(z + \bar{z})^2}{\alpha^2} - \frac{(z - \bar{z})^2}{\beta^2} = 4\\ &\iff \lambda(z^2 + \bar{z}^2) + 2(1-\mu)z\bar{z} = 4\end{align}\tag{*1}$$ where $\displaystyle\;\lambda = \frac{1}{\alpha^2} - \frac{1}{\beta^2}$ and $\displaystyle\;\mu = 1 -\frac{1}{\alpha^2} - \frac{1}{\beta^2}$.
It is not hard to show under inversion with respect to the unit circle, point $Z$ get mapped to midpoint of $U$ and $V$. In terms of corresponding complex numbers, we have
$$\frac{1}{\bar{z}} = \frac{u+v}{2} \implies \bar{z} = \frac{2}{u+v} \implies z = \frac{2uv}{u+v}$$
Substitute this into ($*1$) and simplify, the condition for $Z$ to lie on the ellipse becomes $\Omega(u,v) = 0$ where $$\begin{align} \Omega(u,v) &= \lambda( \lambda(1 + u^2 v^2 ) + 2(1-\mu)uv - (u+v)^2)\\ &= \lambda( (\lambda u^2 - 1)v^2 - 2\mu uv + (\lambda - u^2))\\ &= (\lambda u^2 - 1)(\lambda v^2 -1 ) - (1 - \lambda^2 + 2\lambda\mu uv) \end{align}$$
Let $E, F, G, H$ be the points on unit circle touching the line segments $QA, AP, PB$ and $BQ$ respectively. Since $A, P, B$ lies on the ellipse, we get
$$\Omega(e,f) = \Omega(f,g) = \Omega(g,h) = 0$$ Notice $\Omega(u,v)$ is symmetric in $u,v$ and is a quadratic polynomial in of its arguments. $e$ and $g$ and roots of the quadratic polynomial $\Omega(f,\cdot)$, By Vieta's formula, we get
$$e + g = \frac{2\mu f}{\lambda f^2 - 1} = \frac{2\mu f(\lambda g^2 - 1)}{1 - \lambda^2 + 2\lambda \mu f g}$$ By a similar argument to $f, h$ and $\Omega(g,\cdot)$, we have
$$f + h = \frac{2\mu g}{\lambda g^2 - 1} = \frac{2\mu g(\lambda f^2-1)}{1 - \lambda^2 + 2\lambda \mu f g}$$ Summing these and rearrange, we find
$$e + h = \left[\frac{2\mu( \lambda fg - 1)}{1 - \lambda^2 + 2\lambda \mu f g} - 1\right](f+g) = - \frac{1- \lambda^2 + 2\mu}{1 - \lambda^2 + 2\lambda \mu f g} (f + g)$$
Taking complex conjugate, invert them and using $fg = \frac{p}{\bar{p}}$, we get $$q = - \frac{1 - \lambda^2 + 2\lambda\mu \bar{f}\bar{g}}{1 - \lambda^2 + 2\mu} p = - \frac{(1-\lambda^2) p + 2\lambda \mu \bar{p}}{1 - \lambda^2 + 2\mu}\tag{*2}$$ If $P = (x_p,y_p)$ and $Q = (x_q,y_q)$, this is equivalent to
$$(x_q, y_q) = \left( -\frac{1 - \lambda^2 + 2\lambda \mu}{1 - \lambda^2 + 2\mu} x_p, -\frac{1 - \lambda^2 - 2\lambda\mu}{1 - \lambda^2 + 2\mu} y_p\right)\tag{*2'}$$
As long as $1 - \lambda^2 + 2\mu \ne 0$, $Q$ lies on the ellipse $\displaystyle\;\frac{x_q^2}{\tilde{\alpha}^2} + \frac{y_q^2}{\tilde{\beta}^2} = 1$ where
$$( \tilde{\alpha}, \tilde{\beta} ) = \left( \alpha \left|\frac{1 - \lambda^2 + 2\lambda \mu}{1 - \lambda^2 + 2\mu}\right|,\; \beta \left|\frac{1 - \lambda^2 - 2\lambda \mu}{1 - \lambda^2 + 2\mu}\right|\right)$$
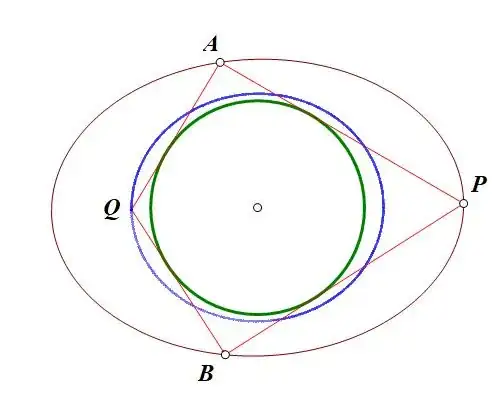
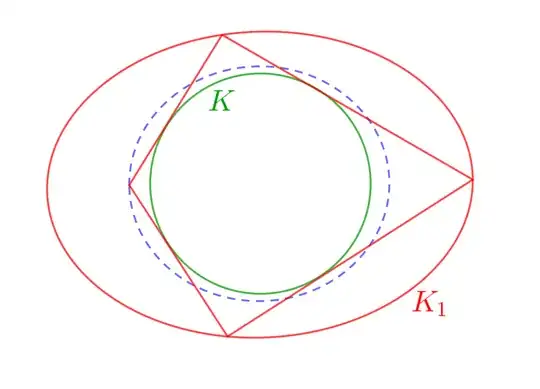
This isn't an answer, it isn't a rigorous proof at all, but a simple numerical experiment.
In particular, copy-pasting the following code in Wolfram Mathematica 12.0:
{xF1ext, yF1ext, xF2ext, yF2ext, V1V2ext} = {1, 0, 6, 5, 10};
{xF1int, yF1int, xF2int, yF2int, V1V2int} = {2, 2, 5, 4, 6};
Δext = V1V2ext^2 - (xF1ext - xF2ext)^2 - (yF1ext - yF2ext)^2;
Δint = V1V2int^2 - (xF1int - xF2int)^2 - (yF1int - yF2int)^2;
If[V1V2ext > 0 && V1V2int > 0 && Δext > 0 && Δint > 0,
a = (xF1ext + xF2ext) / 2;
b = Sqrt[Δext + (xF1ext - xF2ext)^2] / 2;
c = 0;
d = (yF1ext + yF2ext) / 2;
e = (xF1ext - xF2ext) (yF1ext - yF2ext) / (4 b);
f = V1V2ext Sqrt[Δext] / (4 b);
xP = a + b Cos[θ] + c Sin[θ];
yP = d + e Cos[θ] + f Sin[θ];
Δextint = Sqrt[(xP - xF1int)^2 + (yP - yF1int)^2] +
Sqrt[(xP - xF2int)^2 + (yP - yF2int)^2] -
V1V2int /. {θ -> 0};
If[Δextint > 0,
g = 4 (V1V2int^2 - (xF1int - xF2int)^2);
h = 4 (V1V2int^2 - (yF1int - yF2int)^2);
i = -8 (xF1int - xF2int) (yF1int - yF2int);
j = 4 ((xF1int - xF2int) (xF1int^2 + yF1int^2 -
xF2int^2 - yF2int^2) - V1V2int^2 (xF1int + xF2int));
k = 4 ((yF1int - yF2int) (xF1int^2 + yF1int^2 -
xF2int^2 - yF2int^2) - V1V2int^2 (yF1int + yF2int));
l = 2 V1V2int^2 (xF1int^2 + yF1int^2 + xF2int^2 +
yF2int^2) - (xF1int^2 + yF1int^2 - xF2int^2 - yF2int^2)^2 - V1V2int^4;
m = (a - b) ((a - b) g + (d - e) i + j) + (d - e)^2 h + (d - e) k + l;
If[m != 0,
n = 2 (a (2 c g + f i) - b (2 c g + f i) +
c ((d - e) i + j) + 2 f h (d - e) + f k) / m;
o = 2 (a (d i + j) - b e i + 2 c (c g + f i) +
d k + g (a^2 - b^2 ) + h (d^2 - e^2 + 2 f^2) + l) / m;
p = 2 (a (2 c g + f i) + b (2 c g + f i) +
c ((d + e) i + j) + 2 f h (d + e) + f k) / m;
q = ((a + b) ((a + b) g + (d + e) i + j) +
(d + e)^2 h + (d + e) k + l) / m;
r = (-3 n^2 + 8 o) / 8;
s = (n^3 - 4 n o + 8 p) / 8;
t = -3 n^4 + 16 n^2 o - 16 o^2 - 16 n p + 64 q;
u = (16 o^2 - 48 n p + 192 q + t) / 256;
Δ = 16 r^4 u - 4 r^3 s^2 - 128 r^2 u^2 + 144 r s^2 u - 27 s^4 + 256 u^3;
If[(Δ > 0 && (r > 0 || t > 0)) || (Δ == 0 && r > 0 && s == 0 && t == 0),
{xP, yP} = Transpose[Table[{xP, yP}, {θ, 0, 2π, π/100.}]];
a = v^2 (x1 + x2);
b = v^2 (y1 + y2);
c = v^2 (x1 + x2 - 2 x3);
d = v^2 (y1 + y2 - 2 y3);
e = (x1 - x2) (x1 + x2 - 2 x3);
f = (y1 - y2) (y1 + y2 - 2 y3);
g = (x1 - x2) (x1 + x2 + 2 x3);
h = (y1 - y2) (y1 + y2 + 2 y3);
i = x1^2 - x2^2 + f;
j = y1^2 - y2^2 + e;
k = v^2 - (x1 - x2)^2;
l = v^2 - (y1 - y2)^2;
m = k - (y1 + y2 - 2 y3)^2;
n = l - (x1 + x2 - 2 x3)^2;
o = 2 (x3 (y1 + y2 - 2 y3) - x1 (y2 - y3) - x2 (y1 - y3));
p = 2 v^2 (x1^2 + y1^2 + x2^2 + y2^2 + 2 x3^2 + 2 y3^2) -
4 (a x3 + b y3) - (e + f)^2 - v^4;
q = (k - (y1 - y2)^2) (m x4^2 + n y4^2 - 2 o x4 y4);
r = o + z Sqrt[p];
num1X = 2 l r^2 x3 + n^2 (a - i (x1 - x2)) + r n (d - (g + f) (y1 - y2));
num1Y = 2 k n^2 y3 + r^2 (b - j (y1 - y2)) + r n (c - (e + h) (x1 - x2));
den1 = 2 (r^2 l + k n^2 - 2 r n (x1 - x2) (y1 - y2));
num2X = 2 l x3 y4^2 + x4^2 (a - i (x1 - x2)) +
x4 y4 (d - (g + f) (y1 - y2)) - v x4 Sqrt[q];
num2Y = 2 k y3 x4^2 + y4^2 (b - j (y1 - y2)) +
x4 y4 (c - (e + h) (x1 - x2)) - v y4 Sqrt[q];
den2 = 2 (v^2 (x4^2 + y4^2) - ((x1 - x2) x4 + (y1 - y2) y4)^2);
{xT1, yT1} = {num1X, num1Y} / den1 /. {v -> V1V2int, x1 -> xF1int, y1 -> yF1int,
x2 -> xF2int, y2 -> yF2int, x3 -> xP, y3 -> yP, z -> -1};
{xT2, yT2} = {num1X, num1Y} / den1 /. {v -> V1V2int, x1 -> xF1int, y1 -> yF1int,
x2 -> xF2int, y2 -> yF2int, x3 -> xP, y3 -> yP, z -> +1};
{xA, yA} = {num2X, num2Y} / den2 /. {v -> V1V2ext, x1 -> xF1ext,
y1 -> yF1ext, x2 -> xF2ext, y2 -> yF2ext, x3 -> xT1,
y3 -> yT1, x4 -> xP - xT1, y4 -> yP - yT1};
{xB, yB} = {num2X, num2Y} / den2 /. {v -> V1V2ext, x1 -> xF1ext,
y1 -> yF1ext, x2 -> xF2ext, y2 -> yF2ext, x3 -> xT2,
y3 -> yT2, x4 -> xP - xT2, y4 -> yP - yT2};
{xT3, yT3} = {num1X, num1Y} / den1 /. {v -> V1V2int, x1 -> xF1int, y1 -> yF1int,
x2 -> xF2int, y2 -> yF2int, x3 -> xA, y3 -> yA, z -> -1};
{xT4, yT4} = {num1X, num1Y} / den1 /. {v -> V1V2int, x1 -> xF1int, y1 -> yF1int,
x2 -> xF2int, y2 -> yF2int, x3 -> xB, y3 -> yB, z -> +1};
num3X = xA xT4 (yB - yT3) - xB xT3 (yA - yT4) +
xA xB (yT3 - yT4) + xT3 xT4 (yA - yB);
num3Y = xA yT3 (yB - yT4) - xB yT4 (yA - yT3) +
xT4 yB (yA - yT3) - xT3 yA (yB - yT4);
den3 = (xA - xT3) (yB - yT4) - (xB - xT4) (yA - yT3);
{xQ, yQ} = {num3X / den3, num3Y / den3};
ellipses = ListLinePlot[{Transpose[{xP, yP}], Transpose[{xT1, yT1}],
Transpose[{xQ, yQ}]}, PlotStyle -> {Blue, Red, Green}];
frames = Table[lines = Graphics[{Black, Line[{Transpose[{xP, yP}][[i]],
Transpose[{xT1, yT1}][[i]], Transpose[{xA, yA}][[i]],
Transpose[{xT3, yT3}][[i]], Transpose[{xQ, yQ}][[i]],
Transpose[{xT4, yT4}][[i]], Transpose[{xB, yB}][[i]],
Transpose[{xT2, yT2}][[i]], Transpose[{xP, yP}][[i]]}]}];
points = Graphics[{Magenta, PointSize[Large],
Point[{Transpose[{xP, yP}][[i]], Transpose[{xQ, yQ}][[i]]}],
Blue, PointSize[Large], Point[{Transpose[{xA, yA}][[i]],
Transpose[{xB, yB}][[i]]}]}];
Magnify[Show[{ellipses, lines, points}, Axes -> False,
AspectRatio -> Automatic], 2],
{i, 201}]
]
]
]
];
Export["image.gif", frames, "AnimationRepetitions" -> ∞];
we get:
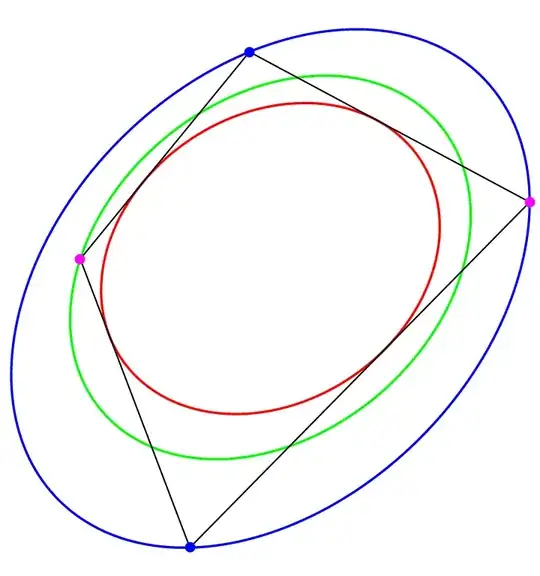
from which we can observe a generic case with any two ellipses. With a simple code change:
{a, b, c, d} = {12, 6, 6, 5};
{xF1ext, yF1ext, xF2ext, yF2ext, V1V2ext} = {-Sqrt[a^2 - b^2], 0, Sqrt[a^2 - b^2], 0, 2 a};
{xF1int, yF1int, xF2int, yF2int, V1V2int} = {-Sqrt[c^2 - d^2], 0, Sqrt[c^2 - d^2], 0, 2 c};
we can refer to the particular case of two ellipses centered and parallel to the Cartesian axis system:
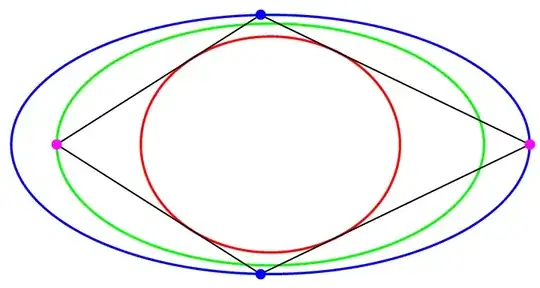
Taking advantage of this code, in symbolic rather than numerical mode, in the latter case the green ellipse, i.e. the locus of the points $(x_Q,\,y_Q)$, is also centered in the origin and has half-axes:
$$ a' = \frac{3\,a\,b^4\,c^4 - 2\,a^3\,b^2\,c^2\,(b^2 + d^2) - a^5\,(b^2 - d^2)^2}{b^4\,c^4 + 2\,a^2\,b^2\,c^2\,(b^2 - d^2) - a^4\,(b^2 - d^2)\,(3\,b^2 + d^2)} \;; \\ b' = \frac{3\,a^4\,b\,d^4 - 2\,a^2\,b^3\,d^2\,(a^2 + c^2) - b^5\,(a^2 - c^2)^2}{b^4\,c^4 + 2\,a^2\,b^2\,c^2\,(b^2 - d^2) - a^4\,(b^2 - d^2)\,(3\,b^2 + d^2)} \;. \\ $$
That's all.
The problem can be generalized so that both curves (the circle and outer ellipse in the diagram) are conics. Then the resulting locus is also a conic. Although the subject matter and concepts are very much that of projective geometry, the methods of proof tend to be more analytic than synthetic.
As described in Andrea Del Centina's Poncelet’s porism: a long story of renewed discoveries (also on JSTOR) the problem was studied in the 19th century, and is related to Poncelet's Theorem.
Look for Fig. 21 in Del Centina's paper (pg 68) which illustrates the approach in George Salmon's On the problem of the In-and-circumscribed Triangle.
Salmon derives an equation for the locus as a weighted sum of the original conics ($U$ and $V$) and a third conic $F$. ($F$ has the remarkable property that the tangents from any point on $F$ to $U$ and $V$ form a harmonic pencil.)
Further on, look for Fig. 31, which illustrates a theorem by Darboux.
A tangential pencil is the set of all conics tangent to a four given lines (some of which may be complex), and is dual to an ordinary conic pencil: the set of all conics containing four given points (some of which may be complex).
If $K_3=K_2=K_1$, the quadrilateral circumscribes $K$ (the inner circle/conic in the question) and three of its vertices lie on $K_1 $ (the outer ellipse/conic), as in the original question (see figure below). Then Darboux's theorem says that the locus of the fourth vertex $Q$ is a conic in the tangential pencil $\mathbf T$ containing $K$ and $K_1$.
To compute the members of $\mathbf T$, let $K'$ and $K'_1$ be the dual conics of $K$ and $K_1$. Then $\mathbf T$ is the set of duals of members of the pencil containing $K'$ and $K'_1$.
Finally, the paper points out that Darboux observed that his theorem was the dual of Poncelet's General Theorem. In the comments, @JeanMarie has pointed out that this question has some similarity with another question math.stackexchange.com/q/3509582. And indeed that one is the dual of this one and is a case of Poncelet's General Theorem.
