circle envelope tangent in another circle

Question

As the picture shows,

One big circle ,$(0,0)$ ,radius=R, there is a small circle in it, $(m,0)$ ,radius=r .

G is on the big circle. From G ,we can do two tangent lines about the small circle. Get the points of intersection E and F. line EF has a envelope about G , which seem like a circle.

How to prove it? Since calculating it requires much effort.

Some additional infomation:

By picking special points,I get

the radius of envelope circle is $$\frac{R \left(m^4-2 m^2 \left(r^2+R^2\right)-2 r^2 R^2+R^4\right)}{\left(m^2-R^2\right)^2}$$

and the circle center $$\left(\frac{1}{2} \left(\frac{R \left(-m^2+2 m R+2 r^2-R^2\right)}{(R-m)^2}-\frac{R \left(-m^2-2 m R+2 r^2-R^2\right)}{(m+R)^2}\right),0\right)$$

Answer 1

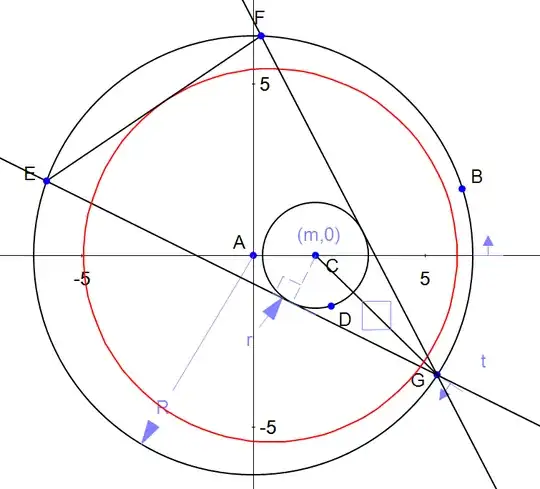
Here is an analytic geometry solution :

We can assume without loss of generality that $R=1$, i.e., we work inside the unit circle. Therefore, we have the following condition : $0 < m <1$.

Let us introduce some notations.

Let $B$ be the second intersection of line $GC$ with the unit circle.

Let $a$ be the polar angle of point $G$ (i.e., oriented angle between positive $x$-axis and $AG$).

Let $b$ be the polar angle of $B$ (i.e., oriented angle between positive $x$-axis and $AB$).

Let $\theta$ be the angle of line $GE$ with line $GB$ (equal to the angle between $GB$ and $GF$).

We will use a certain number of trigonometric formulas. An extensive and well structured list of those can be found here.

Fig. 1: $G(\cos a,\sin a)$, $B(\cos b,\sin b)$, and $C(m,0)$, center of the small circle with radius $r$. The circle to which lines $EF$ are all assumed to be tangent is in red.

Let us look for relationships between angles $a,b$ and $\theta$ and lengths $m$ and $r$.

• a) The fact that $GE$ and $GF$ are tangent to the small circle is expressed by the following relationship :

$$\sin \theta = \dfrac{r}{GC}$$

which is equivalent to :

$$(\sin \theta)^2 = \dfrac{r^2}{GC^2}= \dfrac{r^2}{(\cos a - m)^2+(\sin a - 0)^2}=\dfrac{r^2}{1 - 2m \cos a +m^2}\tag{1}$$

• b) The angle between $AE$ and $AB$ is $2 \theta$ by central angle theorem. The same for the angle between $AB$ and $AF$. Let $I$ be the intersection point of line $AB$ and line $EF$ ; triangle $EAF$ being isosceles, line segment $AI$ is orthogonal to $EF$, implying that its algebraic measure ("signed distance") is $AI=\cos(2 \theta)$ (possibly negative).

Therefore, straight line $EF$ whose normal vector is $\vec{AB} = \binom{\cos b}{\sin b}$ has equation :

$$x \cos b + y \sin b = \cos 2 \theta \tag{2}$$

Using relationship $\cos 2 \theta=1-2 \sin^2 \theta$ with formula (1) :

$$x \cos b + y \sin b = 1-\dfrac{2 r^2}{1 - 2m \cos a +m^2}\tag{3}$$

• c) Let us, finally, express that $G, C$ and $B$ are aligned. This relationship, written under the form (see http://mathworld.wolfram.com/Collinear.html) :

$$\begin{vmatrix}m &\cos a &\cos b\\0 & \sin a&\sin b\\1&1&1\end{vmatrix}=0\tag{4}$$

i.e.,

$$m=\dfrac{\sin(a-b)}{\sin a - \sin b}$$

$$\iff \ \ m=\dfrac{\color{red}{2 \sin(\tfrac12(b-a))}\cos(\tfrac12(b-a))}{\color{red}{2 \sin(\tfrac12(b-a))}\cos(\tfrac12(b+a))}=\dfrac{1+\tan(a/2) \ \tan(b/2)}{1-\tan(a/2) \ \tan(b/2)}$$

yielding the rather unexpected following condition :

$$\tan(a/2) \ \tan(b/2)=k \ \ \text{where} \ \ k:=\dfrac{m-1}{m+1}\tag{5}$$

from which we deduce (using a "tangent half-angle formula" and setting :

$$t:=\tan(b/2)$$

that :

$$\cos a=\dfrac{1-\tan(a/2)^2}{1+\tan(a/2)^2}=\dfrac{1-\left(\tfrac{k}{t}\right)^2}{1+\left(\tfrac{k}{t}\right)^2}=\dfrac{t^2-k^2}{t^2+k^2}\tag{6}$$

Plugging (6) into formula (3), we get for the RHS of (3) after some algebraic transformations :

$$\cos 2 \theta=1-\dfrac{2r^2(t^2(m+1)^2+(m-1)^2)}{(m^2-1)^2(1+t^2)}$$

Using once again tangent half-angle formulas, we can now express the equation of straight line $EF$ under the following parametric form in variable $t$ :

$$x \dfrac{1-t^2}{1+t^2} + y \dfrac{2t}{1+t^2} - 1+\dfrac{2r^2(t^2(m+1)^2+(m-1)^2)}{(m^2-1)^2(1+t^2)}=0.\tag{7}$$

It remains to establish that the distance $d$ of the point with coordinates

$$C'(x_0,y_0)=\left(4m\dfrac{r^2}{(1-m^2)^2},0\right)\tag{8}$$

(would-be center of envelope circle) to straight line $EF$ is constant (i.e., is independent from $t$).

This distance, obtained (see http://mathworld.wolfram.com/Point-LineDistance2-Dimensional.html) by replacing $(x,y)$ in the Left Hand Side of equation (7) by the coordinates $(x_0,y_0)$ of $C'$ given by (8)

$$d=(2r^2(1+m^2) - (m^2 - 1)^2)/(m^2 - 1)^2\tag{9}$$

is indeed independent from parameter $t$ ; moreover it is (up to its sign) the awaited expression (I have used a Computer Algebra System to obtain this expression of $d$).

Remarks :

1) It is possible to characterize the tangent point of $EF$ on the (red) envelope circle, following the method outlined by @Jan-Magnus Økland in comments following this answer.

2) About a possible more (synthetic) geometry solution. I just discovered in this paper dealing with "exponential pencils of conics" that there is so-called "conjugate conic" of the first circle vs. the second circle (see Theorem 2.5 page 4). But I am not sure it will permit a new solution.

---

Answer 2

The expository paper Poncelet's theorem by András Hraskó very nicely treats this problem and its relation to Poncelet's Closure Theorem.

In the OP diagram call the big and little circles $e$ and $a$ respectively, and the red circle $c$. (this corresponds to the labels in the paper, see Figures 1,4,5). Poncelet's Theorem is concerned with scenarios such as Figures 1 and 4, where a polygon is inscribed in $e$ such that the edges touch $a$. But the paper speculates that Poncelet studied that situation of an inscribed triangle where one of the sides does not touch $a$, and found that the non-touching side generates the envelope of a circle $c$ (Figure 5). As @Blue has noted in the comments, $c$ is coaxal with the pair $a$ and $e$.

I leave the details to the paper, but can't resist quoting this:

Poncelet's General Theorem: Let $e$ be a circle of a non-intersecting pencil and let $a_1,a_2,\ldots,a_n$ be (not necessarily different) oriented circles in the interior of $e$ that belong to the same pencil. Starting at an arbitrary point $A_0$ of the circle $e$, the points $A_1,A_2,\ldots,A_n$ are constructed on the same circle, such that the lines $A_0A_1, A_1A_2, \ldots, A_{n-1}A_n$ touch the circles $a_1,a_2,\ldots, a_n$, respectively, in the appropriate direction. It may happen that at the end of the construction, we get back to the starting point, that is, $A_n=A_0$. The theorem states that in that case, we will always get back to the starting point in the $n$-th step, whichever point of $e$ we start from. We do not even need to take care to draw the tangents to the circles in a fixed order.

The case of $a_1=a_2=\cdots=a_n=a$ gives the classic Poncelet's Closure Theorem.

The case $a_1=a_3=a, a_2=c$ relates to the OP.