Understanding initial example in "Mathematical Explanation for the Repertoire Method"

Question

I am working my way through this excellent answer and the first section "Repertoire method (some basics)" (and associated concrete example) I am having trouble following. The crux is that an equation with the additive term

$$ \alpha a_n+\beta b_n $$

will have the solution

$$ \alpha x_n + \beta y_n $$

We are conveniently provided with two recurrences in the repertoire

$$ \begin{align*} x_0&=3&y_0&=1\\ x_n&=3+x_{n-1},\quad n>0&y_n&=5n^2+1+y_{n-1},\quad n>0 \end{align*} $$

to which, via linearity, the solution of the recurrence

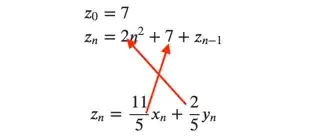
$$ \begin{align*} z_0&=7\\ z_n&=2n^2+7+z_{n-1} \end{align*} $$

is going to be

$$ \begin{align*} z_n=\frac{11}{5}x_n+\frac{2}{5}y_n \end{align*} $$

What steps did were taken to get to that solution? I know it'll be plugging in the provided recurrences somehow and then doing algebraic manipulations but I'm not quite getting it.

PS: I appreciate how friendly, welcoming, and patient the Math SE community has been with my very basic questions so far.

Answer 1

My confusion was caused by the fact that I had it backwards as to which closed form term is associated with which recurrence term. I see now that it is as follows

Which made it much clearer - I can see now how the "scaling factors" to apply to the repertoire were arrived at. For completeness I will outline the steps I took here in the hopes it'll be useful for someone else.

$n^2$ Term

We're looking for our mysterious "factor" that'll linearly combine with our repertoire to give the $2$ target recurrence coefficient. So, representing our mysterious factor as $\alpha$

$$ 5\alpha=2 $$ $$ \alpha=\frac 25 $$

Constant Term

Again, we're looking for something to linearly combine with our repertoire to give the $7$ from the recurrence. We can represent that mysterious factor as $\beta$ that'll scale the repertoire's "$3$" term; so $3\beta$. Thus the equation to find $\beta$ will be $\beta + \alpha = 7$. We already know $\alpha$ is $\frac 25$ so

$$ \begin{aligned} 3\beta + \frac 25&=7\\ 15\beta+2&=35\\ 15\beta&=33\\ \beta&=\frac {33}{15}\\ \beta&=\frac {11}{5} \end{aligned} $$

Closed form

Then the closed form is constructed using these "factors":

$$ \begin{align*} z_n=\frac{11}{5}x_n+\frac{2}{5}y_n \end{align*} $$