How to show that $S^1\sim\Bbb R$, where $S^1=\{(x,y)\in\Bbb R^2,x^2+y^2=1\}$?. I want to show that $S^1$ is uncountable set.
-
3Uncountable is not the same as equipotent with $\Bbb R$. – Asaf Karagila Apr 06 '13 at 17:47
-
@AsafKaragila: In my book, it is asked to show that s1 is uncountable. Is it printed wrong? – Basil R Apr 06 '13 at 17:49
-
1Basil, $\Bbb R$ is uncountable. And showing that $A\sim\Bbb R$ is indeed a way of showing that $A$ is uncountable. But there are uncountable sets which are strictly larger than $\Bbb R$. – Asaf Karagila Apr 06 '13 at 17:52
-
@AsafKaragila: Oh I see. I got your point. You mean $P(\Bbb R)$, the power set? Good to remark it. – Basil R Apr 06 '13 at 17:54
-
1You could also use the fact that you already know, and conclude that if $S^1$ was countable then $\Bbb R$ would be a countable union of countable sets. – Asaf Karagila Apr 06 '13 at 17:55
-
@AsafKaragila: Oh yes, I am sooooo lazy Asaf. I had it before. :-( Thank you – Basil R Apr 06 '13 at 17:57
-
Note also that this bijection is called stereographic projection. – Metin Y. Apr 06 '13 at 19:07
-
@BasilR : You need to clarify your question. "$S^1 ~ \mathbf{R}$"is a stronger statement than "$S^1$ is an uncountable set". Which statement do you need to prove? (Sorry, I don't know how to make the big "tilde" in $\LaTeX$) – Stefan Smith Apr 07 '13 at 18:18
2 Answers
The map $[0,1)\to S^1$ given by $$t\mapsto(\cos 2\pi t,\sin 2\pi t)$$ is a bijection. Do you know the result that $\Bbb R$ is equinumerous to any non-degenerate real interval?
- 105,149
-
-
2Good. You should be able to easily determine a bijection between $(-1,1)$ and $(0,1)$. Now, let $$A=\left{1/n:n\in\Bbb Z,n\ge 2\right}$$ and consider the map $[0,1)\to(0,1)$ given by $$t\mapsto\begin{cases}1/(n+1) & t=1/n\in A\1/2 & t=0\t & \text{otherwise}.\end{cases}$$ That is also a bijection, as you should be able to show. – Cameron Buie Apr 06 '13 at 17:53
Consider the following map from $\mathbb{R} \to S^1$. $$(x,y) = \left(\dfrac{2t}{t^2+1}, \dfrac{t^2-1}{t^2+1} \right)$$ The above map is nothing but the intersection of the line joining the points $(0,1)$ and $(t,0)$ with the circle.
EDIT Below is the picture. As you can see from the picture, $t \in [-1,1]$ maps the part of the circle below the $X$ axis and $t \in ]-\infty,-1] \cup [1,\infty[$ maps the upper part of the circle except the topmost point $(0,1)$. You need throw in the top point, i.e., the point $(0,1)$ separately. Once you do this, we have the one-point compactification of the real line.
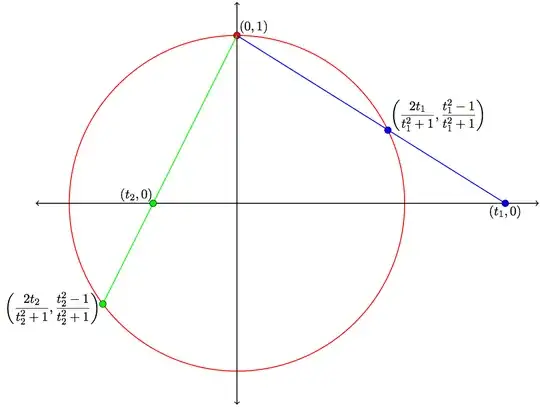
-
1Let $t=\tan\theta$ to unveil the mystery! I don't see why you write $(x,y)$ though. Why not just $f(t)=\cdots$? Might confuse some people. – Pedro Apr 06 '13 at 18:49
-
@PeterTamaroff Why do you think $(x,y) = \left(\dfrac{2t}{t^2+1},\dfrac{t^2-1}{t^2+1}\right)$ would confuse people? – Apr 06 '13 at 21:17