Let
$$f(x,y,z)=a_1 x^4+a_2 x^3+a_3 x^2+a_4 x^2y+a_5 x^2z+a_6 y^2+a_7 z^2+a_8 xy+a_9 xz+a_{10} yz+a_{11}x+a_{12}y+a_{13}z$$
be a polynomial of degree $4$. Can we determine coefficients $a_1, \dots, a_{13}$ such that $f(x,y,z) \ge 0$ for all $x,y,z\in\mathbb{R}$?
Any reference (in particular, a systematic approach to solve such problems), suggestion, idea, or comment is welcome. Thank you!
As mentioned in the comments, this can be (conservatively) posed as a sum-of-squares problem.
Here is an implementation in the MATLAB Toolbox YALMIP which has SOS support (disclaimer, I'm the dev)
sdpvar a1 a2 a3 a4 a5 a6 a7 a8 a9 a10 a11 a12 a13
sdpvar x y z
f = a1*x^4+a2*x^3+a3*x^2+a4*x^2*y+a5*x^2*z+a6*y^2+a7*z^2+a8*x*y+a9*x*z+a10*y*z+a11*x+a12*y+a13*z
params = [a1 a2 a3 a4 a5 a6 a7 a8 a9 a10 a11 a12 a13];
solvesos([sos(f), sum(params) == 1])
The constraint on the sum is added to avoid the trivial zero solution
The polynomial has a lot of structure, so the resulting SDP is pretty small (only 4 monomials are required in the basis)
We can use the Newton polytope. A positive polynomial should have a convex hull defined by even degree monomials. Our polynomial has a polytope representation as can be observed in the following plot.
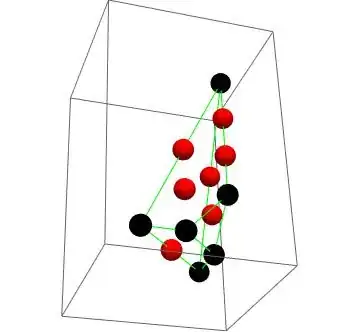
In black the convex hull monomials which are
$$ \left[ \begin{array}{ccc} x & y & z\\ 4 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 2 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \\ \end{array} \right] $$
and in red the inner monomials which are.
$$ \left[ \begin{array}{ccc} x & y & z\\ 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \\ 2 & 0 & 0 \\ 2 & 0 & 1 \\ 2 & 1 & 0 \\ 3 & 0 & 0 \\ \end{array} \right] $$
Accordingly we should have $a_{11}=a_{12}=a_{13}=0$. After that, the polytope is represented as
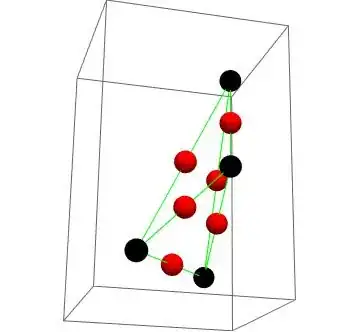
Now the convex hull is formed by
$$ \left[ \begin{array}{ccc} x & y & z\\ 4 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 2 \\ 2 & 0 & 0 \\ \end{array} \right] $$
and this arrangement has chance of positivity. To proceed we can obtain this convex hull
$$ \{x^4,\ x^2,\ y^2,\ z^2\} $$
using a convenient monomial basis as
$$ \{x^2,\ x,\ y, \ z\} $$
so our polynomial form can be represented as
$$ f(x,y,z) = Z^{\dagger}B Z $$
with $Z = \{x^2,\ x,\ y, \ z\}^{\dagger}$ and $B$ a $4\times 4$ matrix of coefficients. At this point we can follow with the analysis performed on the comment references.
NOTE
After the $B$ determination (definite positiveness) we have the relationships
$$ \left\{ \begin{array}{rcl} b_{4,4}&=&a_1 \\ b_{3,4}+b_{4,3}&=&a_2 \\ b_{2,4}+b_{4,2}&=&a_4 \\ b_{1,4}+b_{4,1}&=&a_5 \\ b_{3,3}&=&a_3 \\ b_{2,3}+b_{3,2}&=&a_8 \\ b_{1,3}+b_{3,1}&=&a_9 \\ b_{2,2}&=&a_6 \\ b_{1,2}+b_{2,1}&=&a_{10} \\ b_{1,1}&=&a_7 \\ \end{array} \right. $$
One approach is to view the polynomial as an affine quadratic form in $(y,z)$ with coefficients that depend on $x$ and the $a_i$'s. For a fixed $x$, the condition that the form in $(y,z)$ is $\ge 0$ is equivalent to some inequalities in $x$ and $a_i$'s. Now impose the condition that those inequalities hold for all $x$ and you should get some conditions for the $a_i$'s (in principle).
However, in this particular case, note that we must have $f(x,0,0)\ge 0$, so $$x(a_1 x^3 + a_2 x^2 + a_3 x + a_{11})\ge 0$$ so this implies $a_{11}=0$.
Now consider $f(0,y,0)\ge 0$ and get $a_{12}=0$. Similarly, from $f(0,0,z)\ge 0$ we ge $a_{13}=0$.
Now write $f=f_4 + f_3 + f_2$, the decomposition into homogenous components. Consider values close to $0$, the dominant contribution is from $f_2$. Therefore, $f_2$ must be a positive semidefinite quadratic form.
Getting back to the idea in the introduction, the Wikipedia article of the types of conic sections is useful. More analysis is needed.
We can give possible solutions for $f$ as follow: $$f = x^2 P(x) + Q_1(x^2, y,z) + Q_2(x,y,z)$$
where $P(x)$ is a positive polynomial of degree $2$, and $Q_1$, $Q_2$ are positive semidefinite quadratic forms.
