I've tried to prove this property of Bessel function but I don't seem to be going anywhere
$$\sqrt{\frac 12 \pi x} J_\frac 32 (x) = \cfrac{\sin x}{x} - \cos x$$
I have tried substituting $\frac 32$ for $J_n (x)$ and then manipulating with the product but it doesn't seem to give me something similar with the series on my LHS. I don't know if there is another different approach which I must follow.
Using the series expansion of $J_{3/2}(x)$ and the Legendre duplication formula for the gamma function, we find $$ \sqrt {\frac{{\pi x}}{2}} J_{3/2} (x) = \sqrt {\frac{{\pi x}}{2}} \left( {\tfrac{1}{2}x} \right)^{3/2} \sum\limits_{n = 0}^\infty {( - 1)^n \frac{{\left( {\frac{1}{4}x^2 } \right)^n }}{{n!\Gamma \left( {n + \frac{5}{2}} \right)}}} \\ = \sqrt \pi \sum\limits_{n = 0}^\infty {( - 1)^n \frac{{x^{2n + 2} }}{{2^{2n + 2} n!\Gamma \left( {n + \frac{5}{2}} \right)}}} = \sum\limits_{n = 0}^\infty {( - 1)^n \frac{{(2n + 2)}}{{(2n + 3)!}}x^{2n + 2} } \\ = \sum\limits_{n = 1}^\infty {( - 1)^{n + 1} \frac{{2n}}{{(2n + 1)!}}x^{2n} } = \sum\limits_{n = 1}^\infty {\frac{{( - 1)^n }}{{(2n + 1)!}}x^{2n} } - \sum\limits_{n = 1}^\infty {( - 1)^n \frac{{x^{2n} }}{{(2n)!}}} \\ = \sum\limits_{n = 0}^\infty {\frac{{( - 1)^n }}{{(2n + 1)!}}x^{2n} } - \sum\limits_{n = 0}^\infty {( - 1)^n \frac{{x^{2n} }}{{(2n)!}}} = \frac{{\sin x}}{x} - \cos x. $$
Using one of the integral representations of Bessel function: $$J_n(x)=\frac{2^{1-n} x^n \int_0^{\frac{\pi }{2}} \sin ^{2 n}t \cos (x \cos t) dt}{\sqrt{\pi } \Gamma \left(n+\frac{1}{2}\right)},$$ We get $$J_{3/2}(x)=\frac{x^{3/2}}{\sqrt{2\pi}}\int_0^{\pi/2}\sin^3t\cos(x\cos t)dt\\ =\frac{x^{3/2}}{\sqrt{2\pi}}\int_0^{\pi/2}(1-\cos^2t)\sin t\cos(x\cos t)dt\\ =\frac{x^{3/2}}{\sqrt{2\pi}}\int_0^1(1-t^2)\cos(xt)dt$$ Can you continue?
Three methods :
1) By using the general (recurrence) formula :
$$J_{\nu-1}(x)+J_{\nu+1}(x)=\frac{2 \nu}{x}J_{\nu}(x)$$
(formula 2.4 p. 13 of this excellent document)
Taking $\nu=\tfrac12$:
$$J_{3/2}(x)=\frac{1}{x}J_{1/2}(x)-J_{-1/2}(x)$$
Knowing that (formulas (2.16) of the document):
$$\begin{align} J_{1/2}(x) = \sqrt{\frac{2}{\pi x}} \sin{(x)}\\ J_{-1/2}(x) = \sqrt{\frac{2}{\pi x}} \cos{(x)} \end{align}$$
we get your result. I assume that $\phi$ is a typo for $\pi$...
2) By using Laplace Transform. Let us prove the equivalent formula :
$$\sqrt{\frac {\pi}{2}} x^{3/2} J_\frac 32 (x) = \sin x - x \cos x \tag{1}$$
As indicated for example in this table,
$$\mathfrak{L}{(x^{\nu}J_{\nu}(x))}=2^{\nu+1}\dfrac{1}{\sqrt{\pi}}\Gamma(\nu+\tfrac12)(s^2+1)^{-\nu-\tfrac12}$$
Knowing the Laplace Transforms:
$$\mathfrak{L}(\sin x)=\frac{1}{s^2+1} \ \ \text{and} \ \ \mathfrak{L}(x \cos x)=\frac{s^2-1}{(s^2+1)^2},$$
it is easy to conclude to the exactness of (1).
3) by taking $n=1$ in the (rather classical) formula :
$J_{p+{\frac{1}{2}}}(x)=\sqrt{\dfrac{2}{\pi}} (-1)^p x^{p+{\frac{1}{2}}} \left(\frac{1}{x}\frac{\mathrm d}{\mathrm dx}\right)^p\left(\frac{\sin x}{x}\right)\tag{2}$
(see this answer, knowing that the spherical Bessel function of order $n$ is defined by :
$$j_n(x):=\sqrt{\dfrac{\pi}{x}}J_{n+\tfrac12}(x)$$
(please note the lowercase $j$).
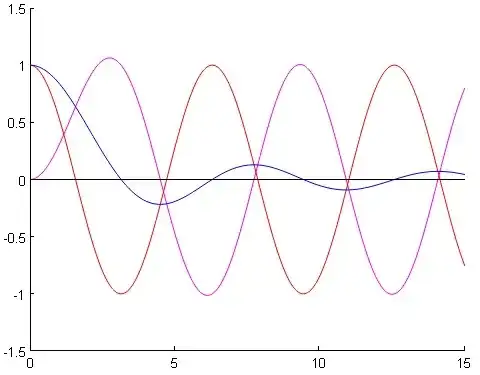
Fig. 1 : Blue curve : $y=$$\text{sinc}$$(x)$, red curve : $y=\cos(x)$, magenta curve : $y=\sqrt{\frac12 \pi x} J_\frac 32 (x)$ Remarks :
1) The roots $r_k$ of Bessel functions in general are important. Here, the roots of $J_{3/2}(x)=0$, are (except $0$) the same as the roots of:
$$\tan x = x \tag{3}$$
These roots have a nice property (please note that we deal only with positive roots):
$$\sum_{k=1}^{\infty} \dfrac{1}{r_k^2}=\dfrac{1}{10}.\tag{4}$$
See proofs of (4) here or here.
2) Connected : the second and third integral of this question.
