I would like to build a function approaching a ramp function with some parameters defining:
I have started to work on this by combining rational and exponential functions, but I have trouble having isolating the very parameters that control all of this...
Hint:
As explained in this related post one of the simplest approximations to the ramp function (which is the integral of the Heaviside step) is the following $$ R(x) = {x \over 2}\left( {1 + {x \over {\sqrt {x^{\,2} + \varepsilon ^{\,2} } }}} \right)\quad \left| {\;\varepsilon < < 1} \right. $$
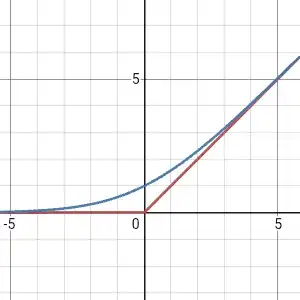
I apologize for the late response. I recently came across this post and as it so happens, I have been experimenting with such functions recently and figured I would add my two-cents.
For my current research, I needed a smooth(ish) approximation to the Heaviside step function defined on a compact interval. I really wanted to use a similar approach to the one discussed in chapter 13 of the book "An Introduction to Manifolds" by Loring W. Tu. This approach uses the function $$f(x)=\left\{\begin{array}{cc}e^{-\frac{1}{x}},&x>0,\\0,&x\le0\end{array}\right.$$ to construct a $C^\infty$ bump function. When I tried implementing this numerically I ran into some problems due to the very fast nature of how this function approaches $0$ (overflow errors, division by zero, etc. ).
This led me to an approach that is extremely similar to that used in the book but instead of using the function $e^{-\frac{1}{x}}$, I needed to find a function with the same basic ''shape'' and behavior as the exponential but which was simpler to compute and used only addition/subtraction, multiplication/division (and was perhaps not $C^\infty$ but just $C^1$ or $C^2$). I thought for a while and finally decided to use the function
$$f(x)=\left\{\begin{array}{cc}1-\frac{1}{1+x^p},&x>0,\\0,&x\le0\end{array}\right.$$ where $p$ is a positive integer greater than or equal to 2.
To construct the Heaviside step function approximation from this you can simply follow a slightly altered version of the procedure in the book by Tu
Define $g(x)=\frac{f(x)}{f(x)+f(1-x)}$ and let $\epsilon$ be the desired width of the smoothed interval around the corner point (in the plots below I use $\epsilon=.1$)
The approximation to the Heaviside-step function is then given by $$H_\epsilon(x)=g\left(\frac{x-\frac{\epsilon}{2}}{\epsilon}\right)$$
Here is a comparison what Tu's Heaviside step function (red) and my Heaviside step function (purple) approximation look like for $p=2$
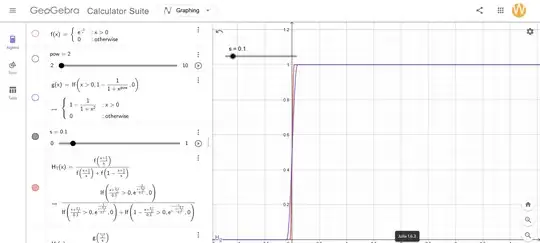
They look very similar and get sharper as you increase the value of $p$. As an added benefit, the function $f$ gains more degrees of smoothness as $p$ is increased.
When I apply this approximation to your desired function $x H(x)$ for $\epsilon=.1$ and $p=4$ the result is visually indistinguishable from the desired result.
I hope this helps you out! Please let me know if you have any questions regarding my approach
For the ramp function you could use as approximation for a real-valued $a>0$: $$f(x)=\begin{cases} \dfrac{x}{1-e^{-ax}},\quad x\neq 0\\ \dfrac{1}{a},\quad x=0 \end{cases}$$ which could be made as closed as desire by increasing the value of $a$. You could see its plot on this question:
Later you could manage its slope just by multiplying it to $f(x)$, and the threshold is just a shift in its argument.
