Smooth approximation of $f(x)=\begin{cases}0&\text{if}\;x<0\\x&\text{if}\;x \geq 0 \end{cases}$

Question

I'd like to find a smooth function to approximate $$f(x)=\begin{cases}0&\text{if}\;x<0\\x&\text{if}\;x \geq 0 \end{cases}$$ This function should be differentiable everywhere. Thanks.

Answer 1

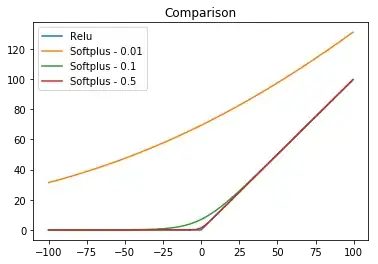
This is the ReLu function. You can approximate it with the softplus function which is given by

$$ f_{t} = \frac{1}{t} \ln(1+e^{tx}) $$

As $\lim_{t \to \infty} f_{t} = f(x) $

Here is some visualization with Python

import numpy as np
import matplotlib.pyplot as plt

def relu(array):
    y = list(map(lambda x: max(0,x), array))

    return y

def softplus(array, t):

    f_t = (1/t)*np.log(1+np.exp(array*t))
    return f_t

my_range = np.arange(start=-100, stop=100, step=0.5)
fig = plt.figure()
ax = plt.subplot(111)
r = relu(my_range)
f_t_01 = softplus(my_range, 0.01);
f_t_1 = softplus(my_range, 0.1)
f_t_5 = softplus(my_range,0.5)
ax.plot(my_range, r, label='Relu')
ax.plot(my_range, f_t_01, label='Softplus - 0.01')
ax.plot(my_range, f_t_1, label = 'Softplus - 0.1')
ax.plot(my_range, f_t_5, label = 'Softplus - 0.5')
plt.title('Comparison')
ax.legend()
plt.show()

Answer 2

From https://www.quora.com/What-smooth-approximations-to-the-ReLu-function-are-available-in-TensorFlow, an approximation is $\frac{1}{t}$ln$(1+e^{tx})$. Here $t$ is a positive number - the larger $t$ is, the more accurate the approximation will be. As $x$ approaches $\pm\infty$, the function will be more accurate. It is most inaccurate at $x=0$, with an error of ln$(2)/t$.