Show that $|\sum_{k=1}^{n} |\sin{(k + \phi)}| \sin{(k + \phi)}| < M^*$

Question

Let $S_n = \sum_{k=1}^{n} [|\sin{(k + \phi)}| \sin{(k + \phi)}] $. Prove that $|S_n| < M(\phi) < M^*$, for all $\phi$ and $n\le 10^9$ (or for any $n$, if you can). $M^*$ must not be a function of $n$, but some given number.

The summand function is an odd function, where the $\pm \sin^2(x)$ changes sign in intervals of $\pi$.

In fact, computer simulations give that $M^* \simeq 1.55$ would be a very tight bound. Note that $S_n $ has alternatingly positive and negative value intervals in $n$. Since the sum's argument $k + \phi$ samples all phase values of the $\sin$-function, the sum has expectation value zero, and maximum variance is limited to a value independent of $n$.

The phase $\phi$ shifts the value range of $S_n$ up and down, resulting in different $M(\phi)$. In fact, it could be demonstrated that there is a lower and an upper bound to $S_n$, and how they behave with $\phi$. If this were an integral, this would be easy to demonstrate, however with the sum, a proof is necessary.

Help is appreciated, also for parts of this problem.

Answer 1

Here is an answer which establishes $M(\phi)$ and $M^* = 1.75$. Some example figures are given at the bottom.

For $S_n$, let's consider the sum's argument $f(x) = |\sin{(x)}| \sin{(x)}$. This can be written as a Fourier series, $$ f(x) = \frac{8}{\pi}\sum_{m=0}^\infty \frac{1}{4(2m+1)-(2m+1)^3} \sin((2m+1)x) $$ Now we can sum $$ S_n = \sum_{k=1}^{n} f{(k + \phi)} = \frac{8}{\pi}\sum_{m=0}^\infty \frac{1}{4(2m+1)-(2m+1)^3} \sum_{k=1}^{n}\sin((2m+1)(k + \phi)) $$ where $$ \sum_{k=1}^{n}\sin((2m+1)(k + \phi)) = \frac{\sin(n(m + \frac12)) \cdot \sin((1 + n + 2 \phi)(m + \frac12)) }{ \sin(m + \frac12)} $$

Now we have the following fact which can be evaluated by computer: we have that $\frac{1}{|\sin(m + \frac12)|}<m$ for almost all $m \in [2,10^9]$, other than very few exceptions, i.e. $m_R \in \{9,12,166,188, 51996, 156344,990063,2136471,40071928,205778993\}$.

Note: The bound can be further tightened, see Jack D'Aurizio's answer in this post which discusses $\frac{1}{\left|\sin m\right|}\leq \frac{\pi/2}{d(m,\pi\mathbb{Z})}$.

This allows to write, with $Q = 10^9$:

$$ S_n = \frac{8}{\pi}[\sum_{m=0}^{1} +\sum_{m=2}^{Q-1} + \sum_{m=Q}^\infty] \frac{1}{4(2m+1)-(2m+1)^3} \frac{\sin(n(m + \frac12)) \cdot \sin((1 + n + 2 \phi)(m + \frac12)) }{ \sin(m + \frac12)} $$ The first two terms evaluate $$ |S_n^{(1)}| = \frac{8}{\pi} |\sum_{m=0}^{1} \frac{1}{4(2m+1)-(2m+1)^3} \frac{\sin(n(m + \frac12)) \cdot \sin((1 + n + 2 \phi)(m + \frac12)) }{ \sin(m + \frac12)}| \\ = \frac{8}{\pi} |\frac13 \cdot \frac{\sin(\frac{n}{2}) \cdot \sin((1 + n + 2 \phi)\frac12) }{ \sin(\frac12)} - \frac{1}{15} \cdot \frac{\sin(\frac{3n}{2}) \cdot \sin((1 + n + 2 \phi)\frac32) }{ \sin(\frac32)}| $$

Now consider $n=x$ and let $x$ be a free real variable. Then we can obtain bounds, dependent on $\phi$, for the function $$f(x) = \frac{8}{\pi}(\frac13 \cdot \frac{\sin(\frac{x}{2}) \cdot \sin((1 + x + 2 \phi)\frac12) }{ \sin(\frac12)} - \frac{1}{15} \cdot \frac{\sin(\frac{3x}{2}) \cdot \sin((1 + x + 2 \phi)\frac32) }{ \sin(\frac32)}) $$

The function $f(x)$ is periodic in $2 \pi$. The mean $\mu(\phi)$ can be easily given as $$ \mu(\phi)= \frac{1}{2 \pi} \int_{0}^{2 \pi}f(x) dx = \frac{4}{15 \pi} (\frac{5 \cos(1/2 + ϕ)}{\sin(\frac12)} - \frac{\cos(3/2 + 3 ϕ)}{\sin(\frac32)} ) $$ The maximum of $\mu(\phi)$ can be computed as $\rho = \frac{8 (2 + 5 \cos(1))}{15 \pi \sin(\frac32)}$. This is also the maximum of the oscillatory part $f(x) - \mu(\phi)$, which is independent of $\phi$. Hence we can bound $$ |S_n^{(1)}| \le \max_{\pm \rho} |\pm \rho + \frac{4}{15 \pi} (\frac{5 \cos(1/2 + ϕ)}{\sin(\frac12)} - \frac{\cos(3/2 + 3 ϕ)}{\sin(\frac32)} )| = M_{\rho}(\phi) \le 2 \rho < 1.601 $$

The value $M_{\rho}(\phi) $ later serves as a component of the bound $M(\phi)$.

For the second part, we can use the above mentioned bound $\frac{1}{|\sin(m + \frac12)|}<m$ for almost all $m \in [2,10^9]$. However, since we sum over $m$, and since the summand is proportional to $\sin(n(m + \frac12)) \cdot \sin((1 + n + 2 \phi)(m + \frac12)) $, we cannot employ a $\phi$-dependent measure here. Instead, we bound $\sin(n(m + \frac12)) \cdot \sin((1 + n + 2 \phi)(m + \frac12)) \le 1 $ and obtain

$$ |S_n^{(2)}| = \frac{8}{\pi} |\sum_{m=2}^{Q-1} \frac{1}{4(2m+1)-(2m+1)^3} \frac{\sin(n(m + \frac12)) \cdot \sin((1 + n + 2 \phi)(m + \frac12)) }{ \sin(m + \frac12)}| \\ \le \frac{8}{\pi}\sum_{m=2}^{Q-1} | \frac{1}{4(2m+1)-(2m+1)^3} \frac{1}{ \sin(m + \frac12)}| \\ \le \frac{8}{\pi} \sum_{m=2}^{\infty} | \frac{m}{4(2m+1)-(2m+1)^3} | + \frac{8}{\pi} \sum_{m_R} |\frac{1}{4(2m_R+1)-(2m_R+1)^3} (\frac{1}{ \sin(m_R + \frac12)} -m_R)| \\ = \frac{7}{15 \pi} + \frac{8}{\pi} \sum_{m_R} |\frac{1}{4(2m_R+1)-(2m_R+1)^3} (\frac{1}{ \sin(m_R + \frac12)} -m_R)| $$ The third part can be bounded, using that $\frac{\sin(n(m + \frac12)) }{ \sin(m + \frac12)} \le n$, with $$ |S_n^{(3)}| = \frac{8}{\pi} |\sum_{m=Q}^{\infty} \frac{1}{4(2m+1)-(2m+1)^3} \frac{\sin(n(m + \frac12)) \cdot \sin((1 + n + 2 \phi)(m + \frac12)) }{ \sin(m + \frac12)}| \\ \le \frac{8}{\pi} \sum_{m=Q}^{\infty} | \frac{n}{4(2m+1)-(2m+1)^3} | \\ \le \frac{2}{\pi} |\frac{n}{4Q^2-1} | $$ and altogether (see the analysis above for $\rho = \frac{8 (2 + 5 \cos(1))}{15 \pi \sin(\frac32)} \simeq 0.8$): $$ |S_n| \le \max_{\pm \rho} |\pm \rho + \frac{4}{15 \pi} (\frac{5 \cos(1/2 + ϕ)}{\sin(\frac12)} - \frac{\cos(3/2 + 3 ϕ)}{\sin(\frac32)} )| + \frac{7}{15 \pi} + \frac{8}{\pi} \sum_{m_R} |\frac{1}{4(2m_R+1)-(2m_R+1)^3} (\frac{1}{ \sin(m_R + \frac12)} -m_R)| + \frac{2}{\pi} |\frac{n}{4Q^2-1} |\\ \le 0.149 + \max_{\pm \rho} |\pm \rho + \frac{4}{15 \pi} (\frac{5 \cos(1/2 + ϕ)}{\sin(\frac12)} - \frac{\cos(3/2 + 3 ϕ)}{\sin(\frac32)} )| = M(\phi) $$

Further (see the analysis above for $\rho$), bounding the term $ \max_{\pm \rho} |\pm \rho + \frac{4}{15 \pi} (\frac{5 \cos(1/2 + ϕ)}{\sin(\frac12)} - \frac{\cos(3/2 + 3 ϕ)}{\sin(\frac32)} )| \le 2 \rho < 1.601$, gives $$ |S_n| \le M(\phi) \le 0.149 + 2 \rho \le 1.75 = M^* $$

$$ \! $$

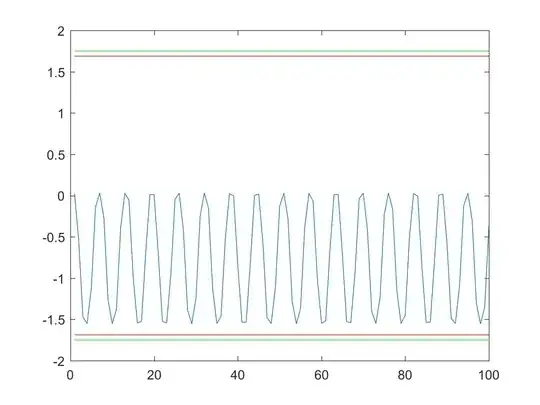
Here are some example figures, where $\pm M(\phi)$ in red, $\pm M^*$ in green, $S_n$ for $n=1 \cdots 100$ in blue (plotted as a continuous graph).

Fig.1: $\phi=0$.

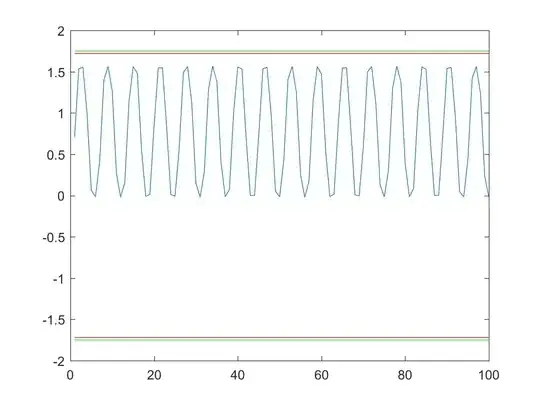
Fig.2: $\phi=1$.

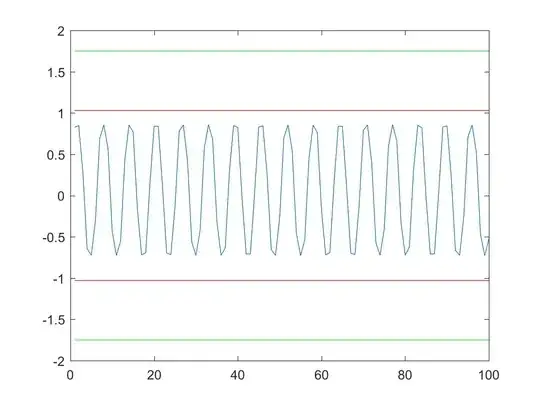
Fig.3: $\phi=2$.