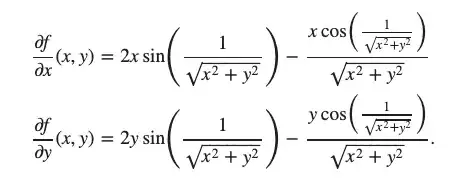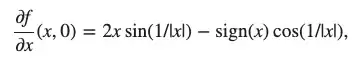2

Let $$f(x,y)=\left\{\begin{array}{l} (x^2+y^2) \sin(\frac{1}{\sqrt{x^2+y^2}}),\:\text{if $(x,y) \not= (0,0)$;}\\ 0,\:\text{if $(x,y)=(0,0)$;} \end{array}\right.$$

Prove that the partial derivatives exist for all $c \in R^2$ but are not continuous in $(0,0)$

My approach:

I have already proved that the partial derivatives exist if $(x,y) \neq (0,0)$. and n the case that $(x,y) = (0,0)$:

\begin{align} \frac {\partial f}{\partial x}(0,0)&=\lim_{t \rightarrow 0} \frac{f[(0,0)+t(1,0)]-f(0,0)}{t}\\ &=\lim_{t \rightarrow 0} \frac{f[(t,0)]}{t} \\ &=\lim_{t \rightarrow 0} \frac{t^2 \sin (1/t)}{t} \\ &=\lim_{t \rightarrow 0} {t \sin (1/t)} \end{align} and due to $\lim_{t \rightarrow 0} t=0$ and $\sin (1/t) \le 1 $ then $=\lim_{t \rightarrow 0} {t \sin (1/t)}=0$

In the same way I can prove that $\frac {\partial f}{\partial y}(0,0)=0$

In order to prove that the partial derivatives are not continuous I must prove that $\lim_{(x,y) \rightarrow (0,0)} \frac {\partial f}{\partial x}(0,0) \neq 0$

I'm stuck here. Any ideas?

Alex Turner
  • 784

1 Answers1

3

Away from the origin, one can use the standard differentiation formulas to calculate that

enter image description here

Both of these derivatives oscillate wildly near the origin. For example, the derivative with respect to $x$ along the $x$-axis is

enter image description here

for $x\neq 0$, where $\operatorname{sign}(x)$ is $\pm1$ depending on the sign of $x$. In this case, the sine term goes to zero near the origin but the cosine term oscillates rapidly between $1$ and $−1$, as it is not multiplied by anything small.

This is an example of differentiable functions with discontinuous partial derivatives. See the analysis in the nice linked article. And also this old question on the site:

Can "being differentiable" imply "having continuous partial derivatives"?