First off, let's be clear on the definition of a parabolic point. In the study of the iteration of an analytic function $f:\mathbb C \to \mathbb C$ we say that a fied point $z_0$ is parabolic if $f'(z_0)$ is a root of unity. In particular, $|f'(z_0)|=1$ so that $f$ is neither repulsive ($|f'(z_0)|>1$) or attractive ($0<|f'(z_0)|<1$) at $z_0$ or super-attractive ($f'(z_0)=0$).
If $z_0$ is either a repulsive or attractive fixed point of $f$, then it turns out that $f$ is dynamically similar near $z_0$ to $g(z)=az$ near zero. In particular, there is a neighborhood of $z_0$ where all points move either away or toward $z_0$ under iteration of $f$. A similar statement can be made when $z_0$ is super-attractive, though that is treated a bit differently.
When we iterate near a parabolic point, we simply don't have that classification. There are at least two concrete properties that we lose that makes analysis more difficult:
- There's no longer a neighborhood where we move either away or toward $z_0$ under iteration of $f$. In fact, there are always some directions where we move towards $z_0$ and other directions where we move away. The exact description of those directions is the content of the Leau-Fatou flower theorem.
- Points move very slowly under iteration near a parabolic fixed point, which makes computer generation of pictures very time consuming.
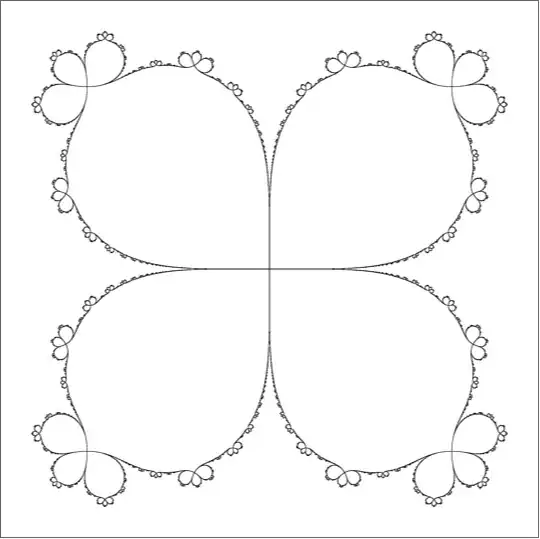
A relatively simple example illustrating all this is given by the function $f(z) = z+z^5$. Note that zero is a parabolic fixed point for this function. If $|r|$ is small, then $|r|^5$ will be very small. Thus, points near zero barely move under application of $f$. This illustrates point 2 above.
To illustrate point 1 above, choose a complex number $z$ in the polar form $z=re^{n\pi i/4}$. Then
$$
f(z) = re^{n\pi i/4} + r^5 e^{5n\pi i/4}.
$$
Note that when $n$ is even, the displacement $z^5$ is in the direction of $z$ and, thus, away from the origin. When $n$ is odd, the displacement $z^5$ is in the opposite direction of $z$ and, thus, toward the origin.
The dynamics of $f$ are illustrated in the following picture:
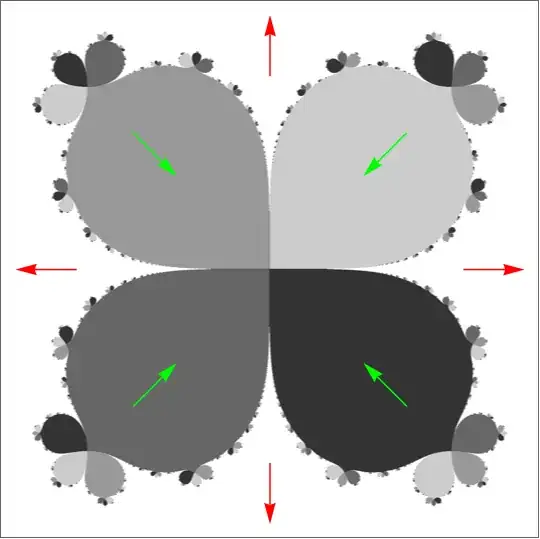
Returning to point 2, the basic escape time algorithm is not particularly good at generating images of these types of Julia sets. A solid understanding of the Leau-Fatou flower theorem, however, allows us to to classify the dynamics based on the repelling/attracting directions. We can then use a boundary scanning technique to generate the following: