Probability of meeting - a confusion

Question

This is a basic probability question.

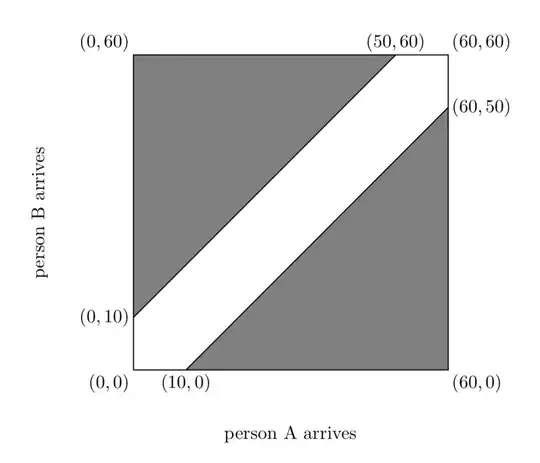
Persons A and B decide to arrive and meet sometime between 7 and 8 pm. Whoever arrives first will wait for ten minutes for the other person. If the other person doesn't turn up inside ten minutes, then the person waiting will leave. What is the probability that they will meet? I am assuming uniform distribution for arrival time between 7 pm and 8 pm for both of them.

The exact question is given here: Probability of meeting

I am aware of geometric probability and the methods they have used there. The answer seems to be unanimously $9/36$. However, here is where I am confused. Considering A reaches before B, and that he reaches before the first $50$ minutes, the probability of meeting should be $5/6 \cdot 1/6= 5/36$ (since B would have to reach within $10$ minutes of A). By symmetry, this means that if B reaches early and reaches before the first $50$ minutes, the meeting probability is again $5/36$. It seems that even without considering the probability of what happens if the earlier person reaches in the last $10$ minutes, we have a probability of $10/36$ already, greater than the total probability calculated in the post in the link.

Can anyone please point out my logical flaw?

Answer 1

There was an arithmetic error in the answer to the linked problem that is the source of your confusion.

If we plot the time person A arrives on the horizontal axis and the time person B arrives on the vertical axis, then the white region in the diagram below represents the band of time in which they arrive within ten minutes of each other, and therefore meet.

The probability that they do not meet is found by dividing the areas of the two grey right triangles by the area of the square.

Each gray right triangle has area $$\frac{1}{2} \cdot 50 \cdot 50$$ so the combined area of the two congruent gray triangles is $$50 \cdot 50$$ The area of the square is $$60 \cdot 60$$ Thus, the probability that persons A and B do not meet is $$\Pr(\text{persons A and B do not meet}) = \frac{50 \cdot 50}{60 \cdot 60} = \frac{25}{36}$$ Subtracting this from $1$ gives the probability that persons A and B do meet, which is $$\Pr(\text{persons A and B meet}) = 1 - \frac{25}{36} = \frac{11}{36}$$ Your method will work.

You calculated that if person A arrives first, then $5/6$ of the time person A will arrive in the first $50$ minutes and that person B has probability $1/6$ of arriving within $10$ minutes of person A. Therefore, should person A arrive first and arrives within $50$ minutes of 7 pm, they have probability $$\frac{5}{6} \cdot \frac{1}{6} = \frac{5}{36}$$ of meeting. By symmetry, if person B arrives first and arrives within $50$ minutes of 7 pm, they have probability $$\frac{5}{36}$$ of meeting.

They will also meet if both of them arrive within the last $10$ minutes of the hour, which occurs with probability $$\frac{1}{6} \cdot \frac{1}{6} = \frac{1}{36}$$ Since these three events are mutually exclusive and exhaustive, the probability that persons A and B will meet is $$\Pr(\text{persons A and B meet}) = \frac{5}{36} + \frac{5}{36} + \frac{1}{36} = \frac{11}{36}$$ which agrees with the answer we obtained above.