6

This is a basic probability question.

Persons A and B decide to arrive and meet sometime between 7 and 8 pm. Whoever arrives first will wait for ten minutes for the other person. If the other person doesn't turn up inside ten minutes then the person waiting will leave. What is the probability that they will meet? I am assuming uniform distribution for arrival time between 7 pm and 8 pm for both of them.

eddie
  • 1,083
  • 1
  • 7
  • 18
  • Look https://math.stackexchange.com/questions/462851/lunch-meeting-probability-for-two-person-to-meet-in-given-1-hour-slot-and-none-w – Elnur Oct 31 '17 at 16:16
  • Related: https://math.stackexchange.com/questions/103015/chance-of-meeting-in-a-bar – Henry Mar 15 '25 at 07:55

3 Answers3

7

My favourite way of solving uniform distribution related problems is to try and think of them in terms of relative volume/area/length. For instance, take a continuous uniform distribution on $[0, 1]$. The probability that $X \in (a, b)$, where $0 \le a \le b \le 1$, and $X$ is a random variable drawn from that distribution, is just the length of the interval $(a, b)$.

Let's do another example. Let $X$ be a uniform distribution over $(0, 5)$. What is the probability that $X \in (a, b)$, where $0 \le a \le b \le 5$?. It is just $\frac{\text{length of interval $(a,b)$}}{\text{length of interval (0, 5)}} = \frac{\text{length of interval $(a,b)$}}{5}$.

This generalizes as well. Let there be a uniform distribution over a square $S$. What is the probability that a randomnly drawn point will be in a particular region $H$?. The answer is $\frac{\text{area of $H$}}{\text{area of $S$}}$.

Let's apply this technique to the current problem.

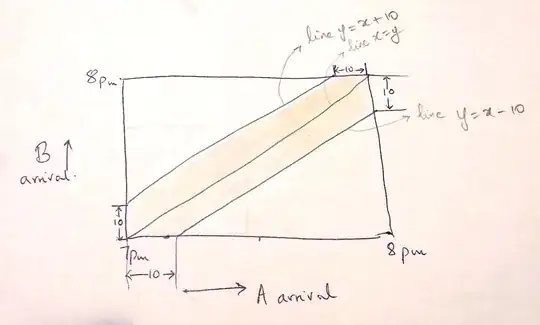
enter image description here

The above picture represents the problem. It is easy to see that the distribution in the question is equivalent to placing a uniform distribution over the square in the diagram, where the times of arrival are the co-ordinates of a randomnly drawn point from the distribution. The shaded are is the favourable area. It represents points $(x, y)$ which are within $10$ of each other. Thus what we need is the area of that region divided by the area of the whole region.

Abhiram Natarajan
  • 1,236
  • 1
    The answer should come out to 9/36 or 3/12. If you think about it in fractions of an hour 10 minutes is 1/6 of an hour, if we make our units 1/6 of an hour the square is 6 units by 6 units = 36 sq. units. The triangles on either side of the "favorable" region is a right triangle with sides of 5 units. The total area of both triangles is 25 sq. units so the favorable area is 36-25 = 9 units. So the area is 9/36 sq. units. – Ravenex Oct 31 '17 at 16:57
  • Thanks. I removed the wrong calculation. – Abhiram Natarajan Oct 31 '17 at 17:04
  • @Ravenex 36-25 is 11 and not 9. So the correct answer should be 11/36. You have made the same mistake in your answer too. – Innocent Feb 02 '20 at 11:08
  • just do $1-(\frac{5}{6)^2=\frac{11}{36}$ – TheCreator Feb 16 '21 at 16:20
0

This problem was already explained here:

Basic probability: Romeo and Juliette meet for a date.

It just needs to be adjusted to work in 6ths instead of 4ths (10/60 of an hour vs. 15/60 of an hour).

The area of the time they don't meet will be 25/36 of the square so the probability they meet will be 9/36.

Ravenex
  • 137
  • 7
-1

I hope your are doing well, I tried a new method to resolve the meeting problem but I didn't find the same result.

We have to calculate $P(|X-Y| < 1/6)$ where X and Y are independents uniformly distributed between 0 and 1.

So : $P(|X-Y| < 1/6) = \int_{0}^{1} \int_{0}^{1} |x - y| * dx*dy$

Then : $P(|X-Y| < 1/6) = \int_{0}^{1} \int_{y - \frac{1}{6}}^{y + \frac{1}{6}} dx*dy$

Finally : $P(|X-Y| < 1/6) = \int_{0}^{1} \frac{1}{3} *dy = \frac{1}{3} $

Please help me to find my error.

Thank you

Bime
  • 9
  • The upper and lower bounds of your integral are wrong. The right integral to evaluate is $\int_{0}^{1} \int_{max(0, y-\frac{1}{6})}^{min(1, y+\frac{1}{6})} dx dy$. Solving this gives 11/36. – Funaizhang Apr 14 '22 at 16:03