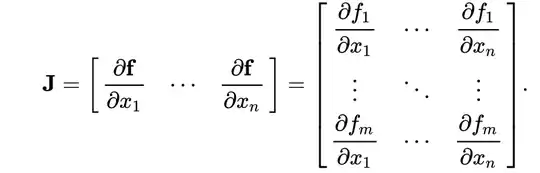Say I have a $ 2 \times 2$ matrix as $A$ and a $2 \times 1$ vector as $X$. I want the derivative of the matrix product with represent to $A$:
Let $y= \begin{bmatrix} a & b\\ c & d \end{bmatrix} \begin{bmatrix} x_1\\ x_2 \end{bmatrix}$
Then what is $\frac{dy}{dA}$?
According to the standard definition of Jacobian 
I should be getting a $ 2 \times 4$ matrix where columns are $a,b,c,d$ but this does not agree with the material I am reading. Is the transpose involved in any of this?
Note that $A\mapsto Ax$ is linear, so everything is trivial.
If you really want to write the Jacobian in coordinates, it's $$ J=\begin{pmatrix} x1 & x2& 0& 0\\ 0& 0&x1&x2 \end{pmatrix} $$ because, as you may check yourself, we have $$ Jvec(B)= Bx $$ for any matrix $B\in\mathbb{R}^{2,2}$ with vectorization $vec({B})\in\mathbb{R}^4$
Begin with the equation and it differential. $$\eqalign{y &= A\cdot x \\ dy &= dA\cdot x}$$ One method to calculate the derivative is to flatten the matrix term using vectorization. $$\eqalign{ dy &= (x^T\otimes I)\cdot da \\ \frac{\partial y}{\partial a} &= (x^T\otimes I) }$$ Another approach is to employ index notation (and Einstein's convention) $$\eqalign{ dy_i &= dA_{ij}\,x_j \\ \frac{\partial y_i}{\partial A_{mn}} &= \bigg(\frac{\partial A_{ij}}{\partial A_{mn}}\bigg)\,x_j = \big(\delta_{im}\delta_{jn}\big)\,x_j = \delta_{im}\,x_n \\ }$$ Yet another idea is to define an isotropic fourth-order tensor as the dyadic product $(\star)$ of two identity matrices $\,({\cal E}=I\!\star\!I)\,$ and dispense with the indices altogether. $$\eqalign{ dy &= dA\cdot x &= ({\cal E}\cdot x):dA \\ \frac{\partial y}{\partial A} &= {\cal E}\cdot x &= I \star x \\ }$$
Remember that matrix calculus can always be re-expressed in non-matrix form by performing the appropriate multiplications. Then you can take the derivatives. This simplified your life a lot (and the overall comprehension) in cases like this one.
Consider that “taking the derivative with respect to a matrix” means de facto taking the derivatives of that expression with respect to each element of the matrix. In this case, you want to derivate $Ax$ by each element of A. Which is trivial if you write down the result of the product $Ax$ and derivate with respect to each of the 4 elements of A. This source can help you understand a little bit better as well as the bottom of page 10 of this matrix cookbook
The Jacobian, the way you wrote it, really only works after vectorizing w.r.t. the components of $A$. More generally, given a function $f\colon X\to Y$, you can think of the derivative as a $(\operatorname{rank} Y, \operatorname{rank} X)$-tensor, which allows one to keep the matrix structure of the input here.
In this case, since the input is a matrix, i.e. a rank-$2$ tensor, and the output is a vector, i.e. a rank-$1$ tensor, you can think of $dy/dA$ the (1, 2) tensor with components
$$\Big(\frac{\rm d y}{\rm d A}\Big)^k_{ij}=\frac{\partial y_k}{\partial A_{ij}} \leadsto D = \frac{\rm d y}{\rm d A} = \begin{bmatrix} \begin{bmatrix} x_1 & x_2 \\ 0& 0\end{bmatrix}, \begin{bmatrix}0& 0 \\ x_1 & x_2\end{bmatrix}\end{bmatrix}$$
This tensor encodes a linear map given by the corresponding tensor contraction
$$D\cdot X = \sum_{ij} D^{k}_{ij} X^{ij}$$
In particular, note that for $f(A)=Ax$ we have the first order Taylor expansion
$$ T_f^{(1)}(A) = f(0) + Df(0)\cdot A =\begin{bmatrix}0 \\ 0\end{bmatrix}+ \begin{bmatrix}A_{11}x_1 + A_{12}x_2 \\ A_{21}x_1 + A_{22}x_2\end{bmatrix} = f(A)$$
I.e. the function is in fact equal to its first order Taylor expansion, as expected, since it's a linear function.
