0

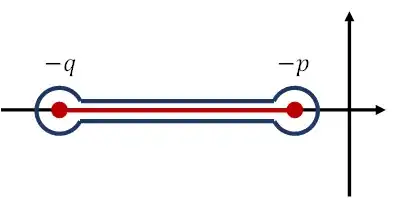
I'm working on computing a contour integral (Actually it's a part of a inverse Laplace transform problem, see my question) $$ \oint_{\Gamma}g(s)ds $$ $$ g(s)=e^{-\tau s\sqrt{\frac{s+q}{s+p}}}e^{ts} $$ where $\tau$, $t$, $p$, $q$ are all positive real, and $q>p$. The integral contour $\Gamma$ can be any contour enclosing the branch cut of $g(s)$, which is the real line segment $(-q,-p)$.

I have tried to evaluate this integral by choosing a bog-bone contour with two key-holes as shown in the picture.

dogbone contour

But it turns out that the contour integrals around the keyhole doesn't zero as the radius of the keyhole $\epsilon\rightarrow 0$ (the integrand seems to behave like $1/\epsilon$).

So my question is how to evaluate the integral around the branch point? Or if it's too difficult should I choose another integral contour?

Yang Xiao
  • 93
  • 1
    $z^{-2} g(1/z)$ is analytic for $0 < |z| < r$ thus your integral is equal to $Res(z^{-2} g(1/z),0)$. But the inverse Laplace transform integral of $e^{-\tau s\sqrt{\frac{s+q}{s+p}}}$ doesn't converge, you'd need to look instead at $s^{-2} e^{-\tau s\sqrt{\frac{s+q}{s+p}}}$. – reuns Aug 01 '19 at 02:18
  • @reuns Thanks very much! First, yes, the integral doesn't converge. Acually I'm now based on Maxim's answer in my previous question post. Could you please give more details on how $s^{-2} e^{-\tau s\sqrt{\frac{s+q}{s+p}}}$ can help solving the ILT problem? – Yang Xiao Aug 01 '19 at 06:24
  • @reuns As for the residue at infinity, I tried to do Laurant expansion and I got this:

    $$ z^{-2}g(z^{-1})=z^{-2}\sum_{n=0}^{\infty}\frac{g^{(n)}(0)}{n!}z^{-n} $$

    In this series, the coefficient of $z^{-1}$ term is 0. I know it's obviously wrong, but I don't know why I'm wrong.

    I'm not a math student and I have only some basic knowledge on complex integral. Appreciate your hints but I'm afraid I need more help.

     – Yang Xiao Aug 01 '19 at 06:26
  • The residue can be written as an infinite sum involving Bell polynomials, but there's still no reason to expect an answer in a closed form. – Maxim Aug 06 '19 at 06:45

0 Answers0