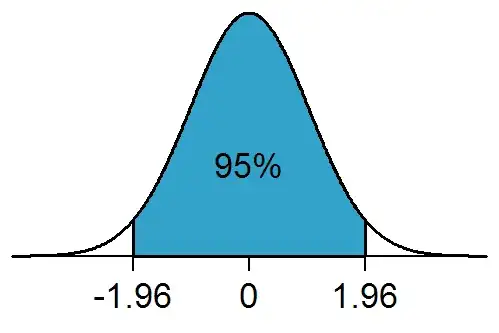
Here's an example from Wikipedia article:
I have a fixed probability $p=0.95$, and I need to find the $X$ for the range symmetric around the mean which limits the normal distribution so that there's a $p$ chance for the value to be in that range.
The inverse CDF, or the probit, can help to find the value which cuts the area into two parts. But I can't get if it can be transformed somehow to get the value for the range?
According to the Wikipedia page, $$\Phi^{-1}(p) = \sqrt2\operatorname{erf}^{-1}(2p - 1)\qquad \text{for} \qquad p\in(0,1)$$ and the problem is the inverse of the error function.
You could get an approximation of $p$ using $$\text{erf}(x)\approx \sqrt{1-\exp\Big(-\frac 4 {\pi}\,\frac{1+\alpha\, x^2}{1+\beta \,x^2}\,x^2 \Big)}$$ where $$\alpha=\frac{10-\pi ^2}{5 (\pi -3) \pi } \qquad \text{and} \qquad \beta=\frac{120-60 \pi +7 \pi ^2}{15 (\pi -3) \pi }$$ which can easily be inversed (at the price of a quadratic in $x^2$.
Othermise, numerical methods such as Newton.
inverffunction will do the job? Then I can use implementation from here: http://www.meta-numerics.net/Samples/FunctionCalculator.aspx Thank you! – astef Jul 01 '19 at 11:28SQRT(GAMMAINV(p,0.5,1)) * SQRT(2)– astef Jul 01 '19 at 11:39