The area enclosed by the locus of point C

Question

Triangle ABC is such that AB = 4, BC = 2, and AC = 3. If vertex A is confined to the x-axis and vertex B is confined to the y-axis, what is the area of the region enclosed by the locus of all points point C could possibly be?

Answer 1

You have some sort of a "do-nothing machine"

The midpoint of $AB$ traces a circle.

Lets start with $B = (0,0), A = (4,0)$ Where is $C$

Area $= \sqrt {(\frac 92)(\frac 52)(\frac 32)(\frac 12)} = \frac {\sqrt {135}}{4}$

$h = \frac {\sqrt {135}}{8}$

And from Pythagoras theorem we get that the altitude splits the base into segments $\frac {11}{8},\frac {21}{8}$

Note there are 2 ways we can orient the triangle at this time.

$(\frac {11}{8},\frac {\sqrt {135}}{4})\\ (\frac {11}{8},-\frac {\sqrt {135}}{4})\\ $

Lets pick $C = (\frac {11}{8},\frac {\sqrt {135}}{4})$ for now.

$A = (4\cos\theta, 0)\\ B = (0, 4\sin\theta)\\ C = (\frac {11}{8}\cos\theta + h\sin\theta, \frac {21}{8}\sin\theta + h\cos\theta)$

$C = (2\cos(\theta - \arctan\frac {\sqrt{135}}{11}), 3\sin (\theta + \arctan \frac{\sqrt {135}}{21}))$

That will trace out something that is roughly an ellipse. I don't think it will be exactly an ellipse.

And swapping the different starting position of $C$ will change the sign on the angle of orientation.

Answer 2

Special Note

Just found out that this is also known as Van Schooten's Locus Problem. Some good references here, here and here. The second references contains a neat solution using a purely geometrical approach.

Additional Note VI (based on Van Schooten's solution)

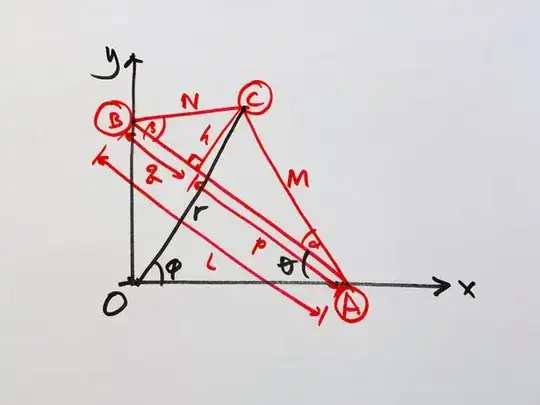
Refer to diagram above.
See Desmos implementation here.

Let $L,M,N$ be the lengths of $AB, AC, BC$ respectively.
Let $Z$ be the midpoint of $AB$.
Note that $ZO=ZA=ZB$.
Let $ZO=ZA=ZB=R(=L/2)$.

Draw a circle centred passing through $A,B,O$. This circle has $Z$ as its centre.
Let $P$ be the point where the line $CZ$ extended meets the circle.
Let $Q$ be the point where the line $ZC$ extended meets the circle.
Hence $ZP=ZQ=R$.

Since the arc $AQ$ is fixed, $\angle AOQ=\angle ABQ $ (fixed). Hence the locus of $Q$ is a straight line $OQ$.
Since the arc $AP$ is fixed, $\angle AOP=\angle ABP $ (fixed). Hence the locus of $Q$ is a straight line $OP$.
And since $PQ$ is a diameter of the circle, $\angle POQ$ is a right angle, i.e. $OP,OQ$ are perpendicular.

Hence the $C$ can be viewed as a point on $PQ$, with $P,Q$ constrained to move along perpendicular lines $OP, OQ$.
Hence $PCQ$ is a Trammel of Archimedes.
Therefore, the locus of $C$ is an ellipse with semi-major/minor axes $CP, CQ$.

Let $w=CZ$. Hence semi-major/minor axes are $$r^*_1=CP=R+w\\r^*_2=CQ=R-w$$ Area enclosed by the locus of $C$ (i.e. the ellipse) is $$\pi \ r^*_1 r^*_2 = \pi (R^2-w^2)\tag{1}$$

Applying the cosine rule on triangles $ZAC, ZBC$: $$\begin{align} w^2&=M^2+R^2-2MR\cos\alpha\\ w^2&=N^2+R^2-2NR\;\cos\beta\\ \text{Adding:}\hspace{3cm}\\ 2w^2&=M^2+N^2-2R(\underbrace{M\cos\alpha+N\cos\beta}_{=L=2R})\\ &=M^2+N^2-2R^2\\ w^2&=\frac {M^2+N^2}2-R^2\\ &=\frac {M^2+N^2}2-\frac {L^2}4\\ \therefore R^2-w^2&=\frac {L^2}2-\left(\frac {M^2+N^2}2-\frac {L^2}4\right)\\ &=\frac {L^2-M^2-N^2}2 \end{align}$$ From $(1)$, area enclosed by the locus of $C$ (i.e. the ellipse) is $$\pi \ r^*_1 r^*_2 = \pi (R^2-w^2)=\color{red}{\pi \left(\frac{L^2-M^2-N^2}2\right)}$$

---

---

Preamble from Original Answer

Interesting problem (+1).

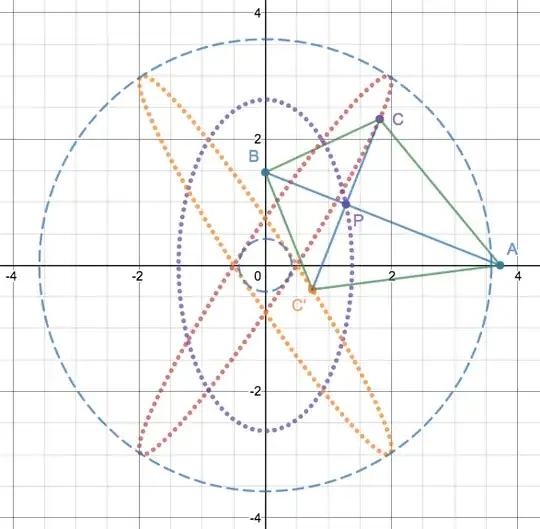
Assuming $A,B$ are confined to the positive $x,y$ axes respectively, this gives two possible positions for $C$, labelled $C, C'$, where $ACBC'$ forms a kite with centre $P$, which divides $AB$ into $p, q$, where $p+q=4$, and semi-wingspan $h$.

Define $\alpha=\angle CAB,\;\; \beta=\angle CBA,\;\; \theta=\angle BAO$.

Using geometry, it can be deduced that, using parameter $\theta$, the coordinates of $C$ are

$$(x,y)=\big(N\cos (\beta\pm\theta),\;\;M\sin(\pm\alpha\mp\theta)\big)$$

where $N=2, M=3$.

Additional Note III

Here's a more straightforward derivation.

$$\begin{align} r^2 &=N^2\cos^2(\beta-\theta)+M^2\sin^2(\alpha+\theta)\\ &=\tfrac12 \big(N^2(1+\cos2(\beta+\theta))+M^2(1-\cos 2(\alpha+\theta))\big)\\ &=\tfrac12 \big(N^2+M^2+N^2\cos2(\beta+\theta)-M^2\cos 2(\alpha+\theta)\big)\\ &=\tfrac 12 \big(N^2+M^2+N^2(\cos 2\beta\cos2\theta+\sin2\beta\sin2\theta)-M^2(\cos2\alpha\cos2\theta-\sin2\alpha\sin2\theta)\big)\\ &=\tfrac12 \big(N^2+M^2+\overbrace{(N^2\cos2\beta-M^2\cos2\alpha)}^A\cos2\theta+\overbrace{(N^2\sin2\beta+M^2\sin2\alpha)}^B\sin2\theta\big)\\ &=\tfrac12 \big(N^2+M^2+\sqrt{A^2+B^2}(\sin\gamma\cos2\theta+\cos\gamma\sin2\theta)\big) \qquad\qquad\qquad\color{grey}{\big(\tan\gamma=\tfrac AB\big)}\\ &=\tfrac12 \big(N^2+M^2+\sqrt{A^2+B^2}\underbrace{\sin(\gamma+2\theta)}_ { \substack{ \text{max: $+1$}\\ \text{min: $-1$} } } \big)\\ {r^*}^2 &=\tfrac12\big(M^2+N^2\pm\sqrt{A^2+B^2}\big)\\ {r_1^*}^2 {r_2^*}^2&=\tfrac14 \big(M^2+N^2-\sqrt{A^2+B^2}\big)\big(M^2+N^2+\sqrt{A^2+B^2}\big)\\ &=\tfrac14 \big((M^2+N^2)^2-(A^2+B^2)\big)\\ &=\tfrac14 \big((M^2+N^2)^2-2(M^2+N^2)L^2+L^4\big) \qquad \text{(see below)}\\ &=\tfrac14 \big((L^2-M^2-N^2\big)^2\\ r_1^*r_2^* &=\frac {L^2-M^2-N^2}2\\ \text{Area of Ellipse}=\pi r_1^*r_2^* &=\color{red}{\pi\left(\frac {L^2-M^2-N^2}2\right)}\\ &=\color{red}{\pi\left(\frac {4^2-3^2-2^2}2\right)}\\ &=\color{red}{\tfrac32\pi}\\\\ \text{NB:}\hspace{3cm}\\ A^2+B^2 &=(N^2\cos2\beta-M^2\cos2\alpha)^2+(N^2\sin2\beta+M^2\sin2\alpha)^2\\ &=M^4+N^4-2M^2N^2(\cos2\alpha\cos2\beta-\sin2\alpha\sin2\beta)\\ &=M^4+N^4-2M^2N^2\cos2(\alpha+\beta)\\ &=(M^2+N^2)^2-4M^2N^2\cos^2(\alpha+\beta)\big)\\ &=\big(M^2+N^2\underbrace{-2MN\cos(\alpha+\beta)}_{M^2+N^2-L^2}\big)\cdot \big(\underbrace{M^2+N^2+2MN\cos(\alpha+\beta)}_{L^2})\big)\\ &=\big(2(M^2+N^2)-L^2\big) L^2\\ \end{align}$$

It can also be shown that the optimal $\theta (\theta^*)$ (i.e. when $C$ is at end of semi-major/minor axes) is given by $$\tan\theta^*=\frac{M^2-N^2\pm L\sqrt{2(M^2+N^2)-L^2}}{\sqrt{(L+M-N)(L-M+N)(-L+M+N)(L+M+N)}}=\frac {\sqrt{15}\pm 4\sqrt{6}}9$$ It is interesting to note that at these positions, the polar angle $\phi$ is the same value as $\theta$, i.e. $$\phi^*=\theta^*$$

---

Additional Note V (Cartesian Form)

The parametric form for the locus of $C$ is $$\big(N\cos(\beta-\theta),\; M\sin(\alpha+\theta)\big)$$

Eliminating parameter $\theta$ gives the Cartesian equation

$$\frac {\big(-xM\sin\alpha+yN\cos\beta\big)^2}{\big(MN\cos(\alpha+\beta)\big)^2}+\frac {\big(xM\cos\alpha-yN\sin\beta\big)^2}{\big(MN\cos(\alpha+\beta)\big)^2}=1$$ which can be transformed into the standard Cartesian form of a rotated ellipse

$$\frac{\big(x\cos\gamma+y\sin\gamma\big)^2}{P^2}+\frac {\big(x\sin\gamma-y\cos\gamma\big)^2}{Q^2}=1$$ where angle of rotation $$\gamma=\arctan\left(\frac{M^2-N^2\pm\sqrt{(M^2+N^2)^2-(2MNcos(\alpha+\beta))^2}}{2MN\sin(\alpha+\beta)}\right)$$ and square of semimajor/minor axes

$$P^2, Q^2=\frac12\left(M^2+N^2\mp\sqrt{(M^2+N^2)^2-(2MN\cos(\alpha+\beta))^2}\right)$$

---

Original Answer (cont'd)

The loci of $C, C'$ are rotated ellipses. The locus of $P$ is an ellipse.

For the loci of $C, C'$, using ideas in the solutions here, it can be further shown that the semi-minor and semi-major axes occur when $r^2 (=x^2+y^2)$ is at a minimum/maximum correspondingly. This occurs when $\theta$ takes on the values $\theta^*_{min}$ and $\theta^*_{max}$ $(=\theta^*_{min} + \frac {\pi}2)$ respectively, where $$\tan 2\theta^*_{min}=-\dfrac {2h}{p-q}=-\tfrac 35\sqrt{15}$$ This gives $$\begin{align} {r^*}^2 &=2^2\cos^2 (\beta-\theta^*)+3^2\sin^2 (\alpha+\theta^*)\\ &=2^2\cdot \tfrac12 (1+\cos2(\beta-\theta))+3^2\cdot\tfrac12 (1-\cos 2(\alpha+\theta))\\ &=\tfrac 12 \big[(2^2+3^2)\mp(p+q)\sqrt{4h^2+(p-q)^2}\big]\\ &=\tfrac 12 \big[13\mp 4\sqrt{10}\big]\\ r^*&=\sqrt{\tfrac{13\mp4\sqrt{10}}2}\\ &=2\pm \sqrt{\tfrac 52}\\ \text{Area of ellipse}\\ \text{ (region enclosed by locus of $C$)} &=\pi \;r^*_1\; r^*_2\\ &=\pi \left(2^2-\tfrac 52 \right)\\ &=\color{red}{\tfrac 32 \pi} \qquad \blacksquare \end{align}$$

Note that the area can also be calculated using $\pi (pq-h^2)$.

See Desmos implementation here.

---

(NB: note that $p=\frac {21}8, q=\frac {11}8, h=\frac 38\sqrt{15}$, $\alpha=\arctan (h/p), \beta=\arctan(h/q)$)

Here's an interesting wikipedia entry on the Trammel of Archimedes, an ellipsograph used for drawing ellipses.

Additional Note I

It is interesting to note that, for the general case, the area of the ellipse, i.e. area bounded by the locus of $C$, is given by $$\color{red}{\pi \left(\frac{L^2-M^2-N^2}2\right)}$$ where $L=AB, M=AC, N=BC$, and the semi-minor/major axes lengths are given by $$r^*=\frac {L\pm \sqrt{2(M^2+N^2)-L^2}}2$$

Also, if $\angle ACB$ is a right angle, i.e. $L^2=M^2+N^2$, then the area is zero, i.e. the locus is a line segment (on the line $y=x$).

---

Additional Note II

This note here shows an alternative derivation.

Let $u=\alpha+\theta, v=\beta-\theta$. Hence $u+v=\alpha+\beta$.

Also, let $m_1=M\sin u,\;\; m_2=M\cos u, n_1=N\sin v,\;\; n_2=N\cos v$.

From above, we have

$$\begin{align} r^2&=N^2 \cos^2 (\beta -\theta)+M^2 \sin^2 (\alpha+\theta)\\ \frac {dr^2}{d\theta}&=2N^2\cos(\beta-\theta)\sin(\beta-\theta)+2M^2\sin(\alpha+\theta)\cos(\alpha+\theta)\\ &=2n_1n_2+2m_1m_2\\ &=0\qquad\qquad\qquad \;\;\text{at max/min }r^2\\ n_1n_2+m_1m_2&=0\\ (n_1n_2+m_1m_2)^2&=0\\ \color{\lightgrey}{m_1^2n_1^2+m_2^2n_2^2}+n_1^2n_2^2+m_1^2m_2^2&=-2m_1m_2n_1n_2+\color{\lightgrey}{m_1^2n_1^2+m_2^2n_2^2}\\ (n_2^2+m_1^2)(n_1^2+m_2^2)&=(m_2n_2-m_1n_1)^2\\\\ \color{\lightgrey}{(n_2^2+m_1^2)^2+2(n_2^2+m_1^2)(m_2n_2-m_1n_1)}\\ +(n_2^2+m_1^2)(n_1^2+m_2^2)&=(m_2n_2-m_1n_1)^2\\ &\;\;\;\color{\lightgrey}{+(n_2^2+m_1^2)^2+2(n_2^2+m_1^2)(m_2n_2-m_1n_1)}\\\\ (\underbrace{n_2^2+m_1^2}+\underbrace{m_2n_2-m_nn_1})^2 &=\big[\underbrace{m_1^2+m_2^2}+\underbrace{n_1^2+n_2^2}+\underbrace{2(m_2n_2-m_1n_1)}\big](\underbrace{n_2^2+m_1^2})\\ \big({r^*}^2+MN\cos(u+v)\big)^2 &=\big(\underbrace{\;\;\;M^2\;\;\;\;\;+N^2+2MN\cos(u+v)}_{L^2}\big)\;\;\;\;\;{r^*}^2\\ \big({r^*}^2+\tfrac {L^2-M^2-N^2}2\big)^2 &=L^2{r^*}^2\\ {r^*}^2-L{r^*}+\underbrace{\tfrac {L^2-M^2-N^2}2}_{\text{Product of roots, }r_1 r_2}&=0\\ \text{Area of ellipse}=\pi\; r_1^* r_2^* &=\color{red}{\pi\bigg(\frac {L^2-M^2-N^2}2\bigg)}\qquad\blacksquare \end{align}$$

NB: $$\small r^*=\frac {L\pm \sqrt{L^2-2(L^2-M^2-N^2)}}2 =\frac {L\pm \sqrt{2(M^2+N^2)-L^2}}2\\$$

---

Additional Note IV (Area of Union of Both Ellipses)
(per OP's additional question in the comments)

The union of the two ellipses (which are of equal area) is twice the area of one ellipse less the area of intersection - the near-diamond-shaped area. The area of one of four equal quadrants is given by

$$Q=\tfrac12r_1r_2\left[\tan^{-1} \big(\tfrac {r_1}{r_2}\cdot\tan\psi_2^*\big)-\big(\tfrac {r_1}{r_2}\cdot\tan\psi_1^*\big)\right]$$ where $\psi_1^*, \psi_2^*$ are the angle between the semimajor-axis in the positive quadrant and the positive $y$-axis and negative $x$-axis respectively. Since $\psi^*=\tfrac \pi 2-\phi^*=\tfrac\pi 2-\theta^*$, this is equivalent to

$$Q=\tfrac12r_1r_2\left[\tan^{-1} \big(\tfrac {r_1}{r_2}\cdot(-\tan\theta^*)\big)-\big(\tfrac {r_1}{r_2}\cdot\cot\theta^*\big)\right]$$

The area of intersection is $4Q$.If $E=$ is the area of one ellipse, the the area of the union of both ellipses is given by $2E-4Q$.