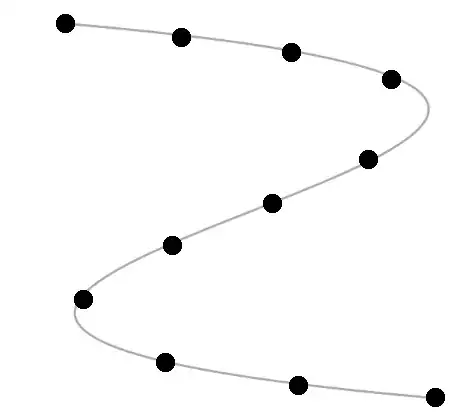
The brute force approach is to just use a polyline approximation. If this is just for graphics, it will certainly be accurate enough. Even for more rigorous applications, it will probably be OK.
Compute a large number of points $n$ along the curve. I'd recommend somewhere in the range $n=50$ to $n=1000$, depending on your accuracy requirements and processor speed. Specifically, let the step-length be $s = 1/n$, and let $t_i = i*s$, and let $P_i = C(t_i)$ be a point on the curve, for $i = 0,1, \ldots , n$. Also, let $c_i = \Vert P_i - P_{i-1} \Vert$ be the $i$-th chord length, and let
$$d_i = \frac{\sum_{j=0}^i c_j}{\sum_{j=0}^n c_j}$$
So, in words, $d_i$ is the fractional distance along the polyline $P_0P_1 \ldots P_n$ at the $i$-th point $P_i$.
Now suppose you want to distribute $m+1$ points $Q_0, \ldots , Q_m$ at equal arclengths along the curve. Here's how you locate the $r$-th point $Q_r$.
Let $d = r/m$. Find $i$ such that $d_{i} \le d \le d_{i+1}$. Then let
$$ u = \frac{d - d_i}{d_{i+1} - d_i} $$
$$ t = t_i + u*s = (i+u)*s$$
$$ Q_r = C(t)$$
Getting all the indexing correct is a chore -- there are lots of opportunities for off-by-one errors. But, other than that, it's straightforward. The basic idea is that distances along the curve can be approximated by distances measured along the polyline $P_0P_1 \ldots P_n$.
You can use your existing code to calculate any point $(x,y) = C(t)$ on the curve.
Here's an implementation in C#:
class Program
{
static void Main()
{
Position endpt0, endpt1, control0, control1;
endpt0 = new Position(100,100); control0 = new Position(200,200);
endpt1 = new Position(100,200); control1 = new Position(400,200);
BezierCurve curve = new BezierCurve(endpt0, control0, control1, endpt1);
// Construct polyline with large number of points
int n = 1000;
double s = 1.0/(n-1);
double[] tt = new double[n];
Position[] PP = new Position[n];
double[] cc = new double[n];
for (int i = 0 ; i < n ; i++)
{
tt[i] = i*s;
PP[i] = curve.Position(tt[i]);
if (i > 0) cc[i] = Distance(PP[i], PP[i-1]);
}
// Get fractional arclengths along polyline
double[] dd = new double[n];
dd[0] = 0;
for (int i = 1 ; i < n ; i++) dd[i] = dd[i-1] + cc[i];
for (int i = 1 ; i < n ; i++) dd[i] = dd[i]/dd[n-1];
// Number of points to place on curve
int m = 10;
double step = 1.0/(m-1);
Position[] QQ = new Position[m];
for (int r = 0 ; r < m ; r++)
{
double d = r*step;
int i = FindIndex(dd, d);
double u = (d - dd[i]) / (dd[i+1] - dd[i]);
double t = (i + u)*s;
QQ[r] = curve.Position(t);
}
}
// Find index i such that dd[i] < d < dd[i+1]
public static int FindIndex(double[] dd, double d)
{
int i = 0;
for (int j = 0 ; j < dd.Length ; j++)
{
if (d > dd[j]) i = j;
}
return i;
}
}