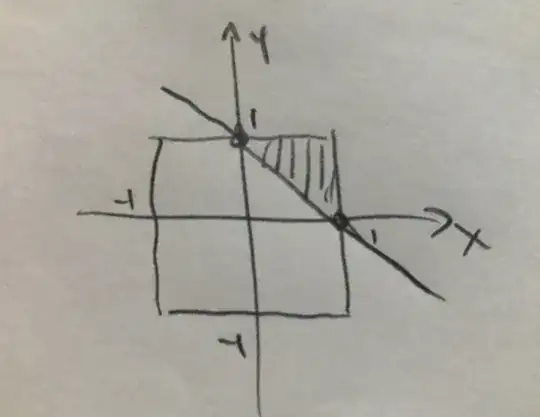
Pick $2$ numbers from $[-1,1]$,what is the probability that their sum is greater than $1$?

Question

Pick 2 numbers from $[-1,1]$, what is the probability that their sum is greater than 1?

It is equal to the probability that the sum of 2 uniform random variables on $[-1,1]$ is greater than 1?

so far,

I got $f(x) = 1/2$ $(-1 < x < 1)$ and $f(y) = 1/2$ $(-1 < y < 1)$, I need to calculate $P(X + Y > 1)$.

I plot the picture of the above convolution, it is a triangle with vertices on $(-2,0),(2,0),(0,1/2)$.

So $P(X + Y > 1)$ is the area to the right side of $x = 1$, which is $1/2 * 1/4 * 1 = 1/8$, is this correct?

Update:Choosing two random numbers in $(0,1)$ what is the probability that sum of them is more than $1$?

Answer 1

I think the quickest way to see this is geometrically. Choosing two points uniformly on $[-1,1]$ is the same as choosing one point uniformly in the box $[-1,1]\times[-1,1]\subset\mathbb{R}^2$. Precisely $\frac18$ of this square is above the line $x+y=1$.

Answer 2

Yes, that is right. An alternative way to get the same answer is to argue as follows. For the sum to exceed $1$, we need both variables to be positive, so $$P(X+Y>1)=P(X,Y>0)\times P(X+Y>1\mid X,Y>0).$$ Now $P(X,Y>0)=\frac12\times\frac12$. Conditioning on this, gives independent uniform variables on $[0,1]$. If $A,B$ independent uniform on $[0,1]$, $A+B>1$ if and only if $(1-A)+(1-B)<1$, and $(1-A),(1-B)$ are also independent uniform on $[0,1]$. It follows that $P(X+Y>1\mid X,Y>0)=\frac12$, giving an overall probability of $\frac12\times\frac12\times\frac12$.