4

I know that for a function $f$ to be differentiable at $a$, the following equality must hold. $$f'(a)=\lim_{x\to a}{\frac{f(x)-f(a)}{x-a}}$$

I also know that the left hand limit differs from the right hand limit at a corner of an absolute value function, so the function is not differentiable at that corner.

I have a question about tropical curves, or for the sake of this question, tropical polynomials.

When plotted, tropical polynomials appear as a piece-wise tropical sum of monomial terms.

More formally, I read here with the emphasis mine:

A tropical polynomial is a piecewise linear function of the form

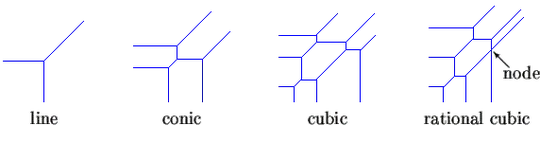
$$T(x,y) = \max_{(i,j)}[{x i + y j + ci,j}] $$ where the calculation is with the usual arithmetic operations and the maximum is taken over a finite subset of $Z^2$ of exponents of $T$ and $c_{i,j}$ are the real number coefficients of $T$. A tropical polynomial $T$ defines a tropical curve, which is the set of points $(x,y)$ where $T(x,y)$ is not differentiable. Here are some tropical curves. enter image description here

Clearly, looking at these tropical curve plots, the limit definition of a derivative must apply (not at corners). Why are tropical curves the set of points $(x,y)$ where $T(x,y)$ is not differentiable if they look like these curves? What am I missing here? One thought is that I am misunderstanding the tropical curve definition. I couldn't find anything on the subject, so my question is are tropical polynomials differentiable?

Second, if they are differentiable, how do you differentiate a tropical polynomial? Are their derivatives analogous to their non tropicalized counterparts just with piece wise restrictions (ie: power rule)?

An example of a tropical polynomial $P$ is given by: $$P(x) = “a\otimes x^3 \oplus b \otimes x^2 \oplus c \otimes x \oplus d"$$ is just a piece wise version of the lines $y=3x+a$, $y=2x+b$, $y=x+c$ and $y=d$ according to Wolfram Demonstrations. All of these lines have derivatives.

Thank you in advance.

Gnumbertester
  • 1,648

1 Answers1

2

A tropical polynomial in two variables $x$ and $y$ is a function $\mathbb{R}^2 \to \mathbb{R}$, so its domain is the $xy$-plane. The tropical curves are the subsets of the $xy$-plane where the tropical polynomial is not differentiable. The curves themselves are not functions, and they are not what we are differentiating. Here when we say "differentiable" it is in the usual sense.

Your example polynomial $P(x)$ would be $P(x)=\min\{0,x,-2x\} = \min\{x,-2x\}$, which is differentiable everywhere except at the point $x=0$. However, this does not define a "curve" in the $xy$-plane, just a point $x=0$ on the $x$-axis.

kccu
  • 21,188