There are at least five ways to multiply two natural numbers $a$ and $b$ given as integer points $A$ and $B$ on the number line by geometrical means. Two of them include counting, the others are purely geometric. I wonder (i) if there are other ways and (ii) how to deeply understand the interrelationship between the different methods (i.e. recipes).
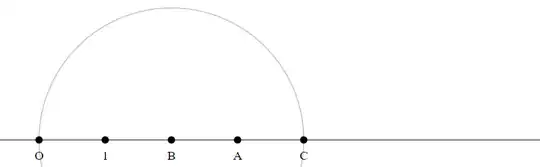
Let $A,B$ be two integer points on the line $O1$:
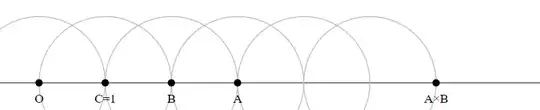
Method 1
- Count how often the unit length $|O1|$ fits into $|OA|$. Let this number be $a$ (here $a = 3$).
Draw a circle with radius $|OB|$ around $B$.
Let $C$ be the (other) intersection point of this circle with the line $O1$.
Draw a circle with radius $|OB|$ around $C$.
Do this $a-1$ times.
The last intersection point $C$ is the product $A \times B$.
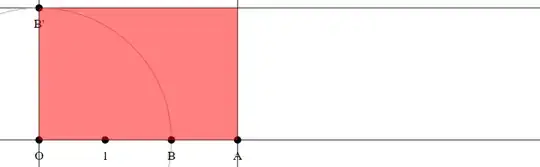
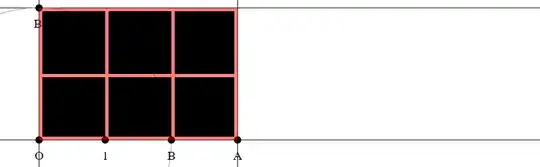
Method 2
- Construct a rectangle with side lengths $|OA|$, $|OB|$.
- Count how often the unit square (with side length $|O1|$) fits into the rectangle. Let this number be $c$ (here $c=6$).
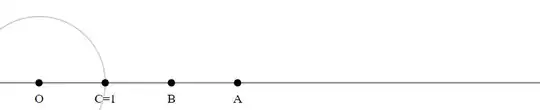
Draw a circle with radius $|O1|$ around $0$.
Let $C$ be the intersection point of this circle with the line $O1$.
Draw a circle with radius $|O1|$ around $C$.
Do this $c$ times.
The last intersection point $C$ is the product $A \times B$.
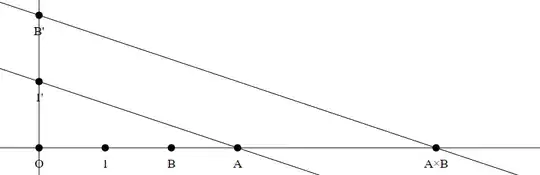
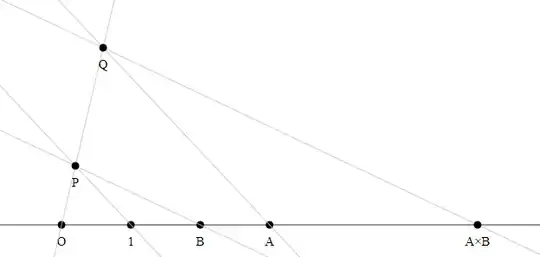
Method 3
Construct the line perpendicular to $O1$ through $O$.
Construct the points $1'$ and $B'$.
Draw the line $1'A$.
Construct the parallel to $1'A$ through $B'$.
The intersection point of this parallel with the line $O1$ is the product $A \times B$.
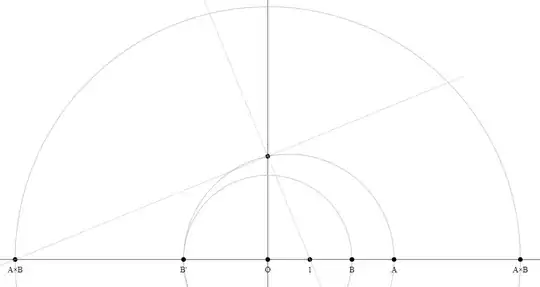
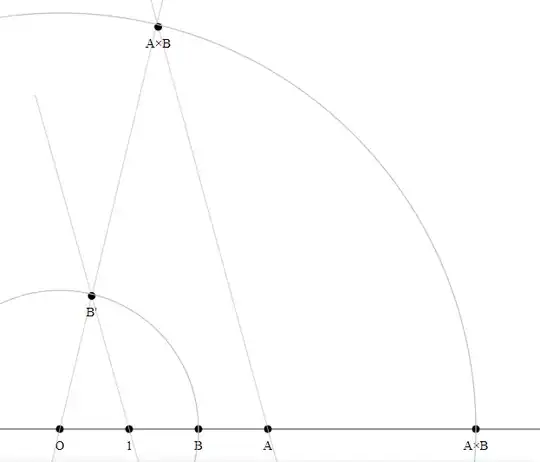
Method 4
Construct the perpendicular line to $O1$ through $O$.
Construct the point $1'$.
Construct the circle through $1'$, $A$ and $B$.
The intersection point of this circle with the line $O1'$ is the product $A \times B$.
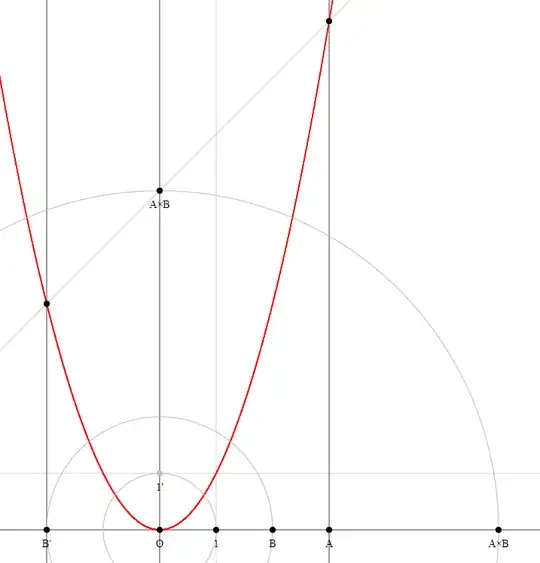
Method 5
This method makes use of the parabola, i.e. goes beyond compass-ruler constructions.
Construct the unit parabola $(x,y)$ with $y = x^2$.
Construct $B'$.
Construct the line perpendicular to $O1$ through $A$.
Construct the line perpendicular to $O1$ through $B'$.
Draw the line through the intersection points of these two lines with the parabola.
The intersection point of this line with the line $O1'$ is the product $A \times B$.
For me it's something like a miracle that these five methods – seemingly very different (as recipes) and not obviously equivalent – yield the very same result (i.e. point) $A \times B$.
Note that the different methods take different amounts $\sigma$ of Euclidean space (to completely show all intermediate points and (semi-)circles involved, assuming that $a >b$):
Method 1: $\sigma \sim ab^2$
Method 2: $\sigma \sim ab$
Method 3: $\sigma \sim ab^2$
Method 4: $\sigma \sim a^2b^2$
Method 5: $\sigma \sim a^3b$
This is space complexity. Compare this to time complexity, i.e. the number $\tau$ of essential construction steps that are needed:
Method 1: $\tau \sim a$
Method 2: $\tau \sim ab$
Method 3: $\tau \sim 1$
Method 4: $\tau \sim 1$
Method 5: $\tau \sim 1$
From this point of view method 3 would be the most efficient.
Once again:
I'm looking for other geometrical methods to multiply two numbers given as points on the number line $O1$ (is there one using the hyperbola?) and trying to understand better the "deeper" reasons why they all yield the same result (i.e. point).
Those answers I managed to visualize I will add here: