Klein-bottle and Möbius-strip together with a homeomorphism

Question

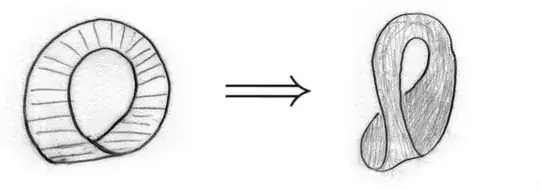
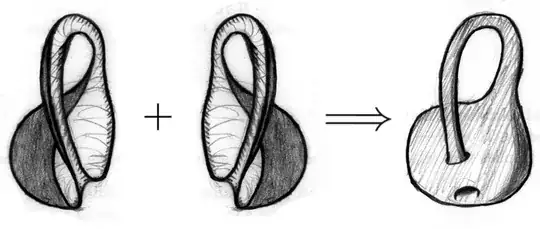
Consider the Klein bottle (this can be done by making a quotient space). I want to give a proof of the following statement:

The Klein Bottle is homeomorphic to the union of two copies of a Möbius strip joined by a homeomorphism along their boundaries.

I know what such a Möbius band looks like and how we can obtain this also by a quotient map. I also know how to see the Klein bottle, but I don't understand that the given statement is correct. How do you construct such a homeomorphism explicitly?

Answer 1

Let's directly glue two Möbius strips into a Klein bottle.

1. Take a Möbius strip and make its bottom wider:

2. Make the rear part of the band like a half of a bottle, also the front part of the band like a tube.

3. Take another Möbius strip and repeat steps 1 & 2 for the new one. Then glue new strip with the old one along their boundaries. Now we get a Klein bottle.

Therefore, a Klein bottle is homeomorphic to the glued Möbius strips.

Answer 2

Present a Klein bottle as a square with vertical edges identified in an orientation-reversing manner and horizontal edges identified in an orientation-preserving manner. Now make two horizontal cuts at one-third of the way up and two-thirds of the way up.

The middle third is one Möbius strip. Take the upper and lower thirds and glue them by the original horizontal identification. This is the other Möbius strip.