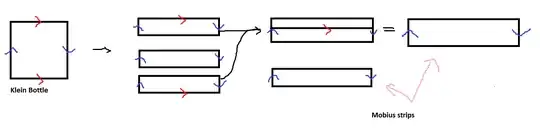
I'm having trouble showing that the Klein bottle defined as a quotient space of $I^2$ with relation $(x,-1)R(x,1)$ and $(-1,y)R(1,-y)$ is Hausdorff and that it can be expressed as $X\cup Y$ where $X,Y$ are homeomorphic to the Möbius strip and $X\cap Y$ is homeomorphic to $S^1$.
Asked
Active
Viewed 1,648 times
8
-
1Your description of $R$ seems to be missing a minus sign on one of the $x$'s or on one of the $y$'s. As it stands, the quotient is not a Klein bottle but a torus. – Andreas Blass Apr 10 '13 at 03:13
-
ah thank you I forgot to include a minus sign on y – user62931 Apr 10 '13 at 12:07
-
2Maybe the picture found here will help you visualize it. – Viktor Vaughn Jun 16 '14 at 00:02