67

During my studies, I always wanted to see a "purely category-theoretical" proof of the Snake Lemma, i.e. a proof that constructs all morphisms (including the snake) and proves exactness via universal properties. It was an interest little shared by my teachers and fellow students, but I have recently found the time to pursue it again.

There is a wonderful book on category theory containing such a proof: The Handbook of Categorical Algebra, Volume 2, by Francis Borceux. I have a question about the proof, however, which I can't seem to resolve.

The Snake Lemma is Lemma 1.10.9, and I have a problem with one of the preliminaries: Namely, the "restricted" Snake Lemma 1.10.8.

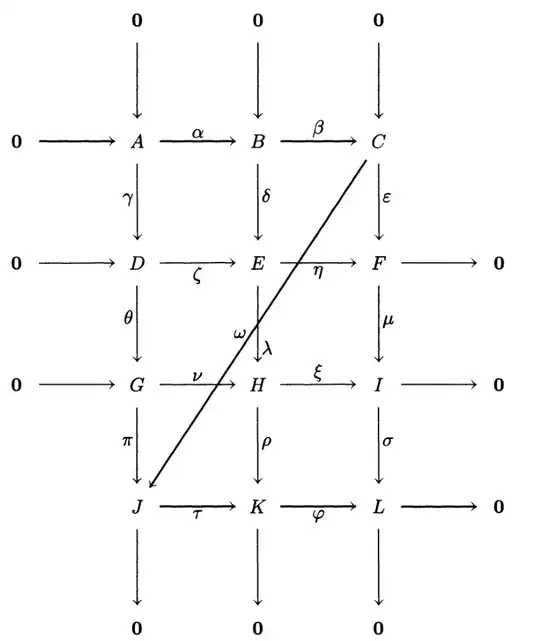
Edit: I scanned the diagrams in question from the book. The following is what we want, i.e. we want to construct $\omega$ from the rest of the diagram where all squares commute and all rows and columns are exact. The claim of the Lemma

The construction is then as follows: $\Delta$ and $\Gamma$ are obtained by pull-back and we define $\Sigma:=\mathrm{Ker}(\Delta)$. Dually with $\Lambda$, $\Xi$ and $\Upsilon$.

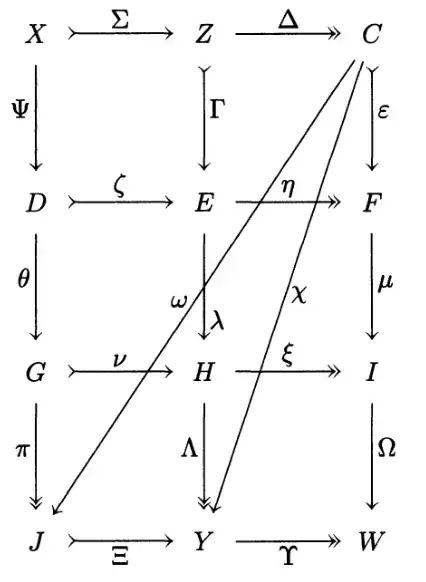
enter image description here

On page 46, he says that

By lemma 1.10.1 and its dual, there are morphisms $\Psi$ and $\Omega$ making the diagram commutative and the outer columns exact.

I can not verify this statement. For instance concerning $\Psi$, it seems to me that in order to apply lemma 1.10.1, one would require that the sequence $(\Gamma,\lambda)$ is exact, but I do not see how that would follow from the construction. What am I doing wrong?!

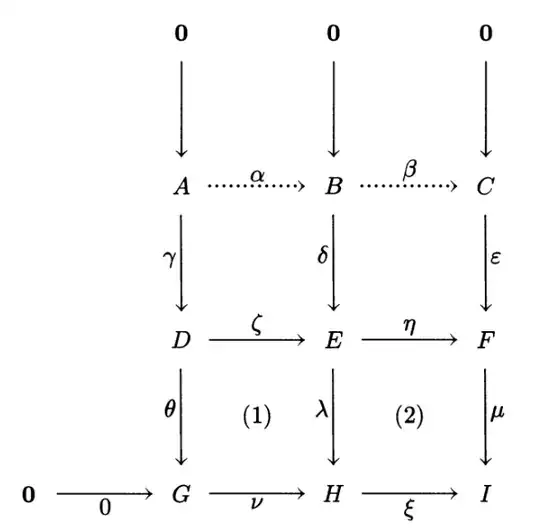
Edit: Lemma 1.10.1 is the statement that in the following diagram, with commutative squares (1) and (2) and exact rows $(\zeta,\eta)$ and $(0,\nu,\xi)$ with $\gamma=\mathrm{Ker}(\theta)$, $\delta=\mathrm{Ker}(\lambda)$ and $\varepsilon=\mathrm{Ker}(\mu)$, there exist unique morphisms $\alpha$ and $\beta$ making the diagram commutative. Additionally, $(\alpha,\beta)$ is exact.

enter image description here

Lehs
  • 14,252
  • 4
  • 28
  • 82
Jesko Hüttenhain
  • 15,116
  • 10
    Simply for your information: Lemma $ 5 $ of Section $ 4 $ of Chapter $ 8 $ of Categories for the Working Mathematician, Second Edition by Saunders Mac Lane also gives a purely categorical proof of the Snake Lemma. :) – Haskell Curry Feb 26 '13 at 08:56
  • 2
    It would be helpful if you could post some pictures of the relevant diagrams, to make the question more self-contained. – Zhen Lin Feb 26 '13 at 13:13
  • @Haskell Curry: Thanks for the tip, but Saunders Mac Lane has never really worked that well for me. If I get no answer to this question I might check it out, but usually I prefer Borceux' writing style. – Jesko Hüttenhain Feb 26 '13 at 16:53
  • 1
    @Zhen Lin: There you go! – Jesko Hüttenhain Feb 26 '13 at 16:54
  • I think you can apply Lemma 1.10.1 by replacing some morphisms with the cokernel of their kernel, e.g. $(\Gamma, \operatorname{coker} \Gamma)$ and $(\epsilon, \operatorname{coker} \epsilon)$. – Zhen Lin Feb 26 '13 at 20:54
  • @Zhen Lin: I don't see how that would work. We could apply the lemma, but we would apply it to a totally different diagram. We could not conclude that $(\Psi,\theta)$ is exact. What we really need is the fact that $\Gamma=\mathrm{Ker}(\lambda)$, and I do not see why this holds. – Jesko Hüttenhain Feb 26 '13 at 22:29
  • That's because it's not true. Take $E = \mathbb{Z}$, $F = I = \mathbb{Z} / 2 \mathbb{Z}$, $H = \mathbb{Z} / 4 \mathbb{Z}$. Rather, what is true is that $\Gamma = \ker (\mu \circ \eta)$. – Zhen Lin Feb 26 '13 at 23:13
  • 6
    @Jesko: Jonathan Wise has written up a direct proof of the Snake Lemma. http://math.stanford.edu/~jonathan/papers/snake.pdf. You can also find a proof in the first paper on abelian categories. Not Grothendieck's Tohoku, but "Exact Categories and Duality" D. A. Buchsbaum, published in 1955. – Martin Brandenburg Mar 09 '13 at 03:27
  • @Martin Brandenburg: +1 and thanks a lot, that looks great. I am still curious if anyone can explain the reasoning in Borceux' book, though. – Jesko Hüttenhain Mar 23 '13 at 18:40
  • You just have to rotate the diagram in Lemma 1.10? Keep in mind that the double headed arrows are epimorphisms (so those show up in the dual of Lemma 1.10) while the special single headed arrows which have arrowheads as their tails are monomorphisms (e.g. $\nu$ in Lemma 1.10). In particular to make things clearer add zeros to the left of X, D, G, J, and add zeros to the right of C, F, I, W. – hasManyStupidQuestions Sep 11 '19 at 03:40
  • 1
    @MartinBrandenburg LINK BROKEN!!! – Daniel Donnelly Sep 24 '23 at 19:56
  • 1
    @DanielDonnelly https://math.colorado.edu/%7Ejonathan.wise/papers/snake.pdf – Lepidopterist Apr 02 '25 at 21:08
  • @Lepidopterist links are funny. Shouldn't all links pass through a web service that fixes the links automatically? By now that's doable, but no such service exists. There are tools to search your personal sites for broken links, but no general web service you pass the link to that always returns the correct link... – Daniel Donnelly Apr 02 '25 at 21:38

1 Answers1

7

In any abelian category you can introduce the notion of element. An element $y$ of an object $Y$ of an abelian category $\mathcal{A}$ is an equivalence class of pairs $(X,h)$, $X \in Ob(\mathcal A)$, $h: X \to Y$ by the equivalence relation $$ (X,h) =(X',h') \iff \exists Z \in Ob(\mathcal A), u:Z \to X, u':Z \to X'\, s.t. \, hu=hu', $$ where $u$ and $u'$ must be epimorphisms. Using the notion of element you can prove the statement in the category of abelian groups. See Gelfand, Manin "Metheods of homological algebra for details.

Daniel Donnelly
  • 22,288
user46336
  • 1,865
  • 13
  • 30
  • 2
    I think the primary interest in the posting of the question was to patch/explain the proof in Borceux (see Jesko's comment on the question from March 23rd). – Mark S. Dec 29 '13 at 19:33
  • 5
    @MarkS. is correct. I primarily want to understand the reasoning in Borceux' book. I hope you don't take my downvote as a personal offense, but this is precisely what I did not want. – Jesko Hüttenhain Dec 29 '13 at 21:08
  • @JeskoHüttenhain It does seem to be a good answer to your title, but not your question "What am I doing wrong?!" However, the convention on math.stackexchange is that a question in the body takes priority, over the title. – Mark S. Dec 29 '13 at 21:10
  • 1
    @user46336 I like your answer because this answers the question I am curious about for so long - why every result proved by diagram chasing in R-Mod is always true in abelian category. For times this seemed to me really mysterious but amazing, just like some principles that always work but cannot be precisely formulated. But now I find this principle could be "exact"(LOL). – Yifeng Huang Jun 06 '14 at 02:36
  • I tried but still have no idea how this works. Could you illustrate it using categories that really have elements, such as abelian groups? – Yifeng Huang Jun 06 '14 at 04:25
  • @YifengHuang May I suggest work on a smaller lemma first using generalized elements to get a feel for them? Starting out at the Snake Lemma is like starting out at the fundamental theorem of Galois theory. – Daniel Donnelly Apr 02 '25 at 21:29
  • @YifengHuang there's a nice old book called "Abelian Categories" by Peter Freyd (whom after the Freyd-Mitchell embedding theorem is named) that's only 87 pages and which can teach you the fundamentals of working with general abelian categories. I'm not sure whether it goes up to the Snake Lemma though. Ping me in chat. I have a copy you could "borrow". – Daniel Donnelly Apr 02 '25 at 21:36