I am following Lang's Algebra on General Homology Theory and wanted to try proving the short exact sequence of complexes $$\require{AMScd} \begin{CD} 0 @>{}>> A @>{f}>> B @>{g}>> C @>{}>> 0 \end{CD}$$ induces a long exact sequence on the homology groups $$\require{AMScd} \begin{CD} @>{}>> H^{i}(A) @>{}>> H^i(B) @>{}>> H^i(C) @>{\delta}>> H^{i+1}(A) @>{}>> H^{i+1}(B) @>{}>> H^{i+1}(C) @>{}>> \end{CD}$$ by the snake lemma. I saw this question regarding the same topic, and I am trying to flesh out the proof by following the comment noting the following diagram commutes and is exact in the rows. $$\require{AMScd} \begin{CD} &&A_n/B(A_n) @>{f_{*}}>> B_n/B(B_n) @>{g_{*}}>> C_n/B(C_n) @>{}>> 0 \\ &@VVV @VVV @VVV \\ 0 @>{}>> Z(A_{n+1}) @>{\alpha}>> Z(B_{n+1}) @>{\beta}>> Z(C_{n+1}) \end{CD}$$ I see how $f$ and $g$ induce homomorphisms $f_*, g_*$ by sending $f_*(a+B(A_n)) = f(a) + B(B_n)$ and similarly for $g$ (at least I think), but I cannot see how the top row is exact. I realize under the induced homomorphism $f_*$ we have $\text{Im}(f_*) = \text{Im}(f)/B(B_n)$ but I'm not sure how to prove this is $\ker(g_*) = g^{-1}(B(C_n))$.
2 Answers
There is probably a quick proof by abstract nonsense, but I can't see that argument right now. However, when in doubt, a diagram chase always works in entry-level homological algebra.
The more difficult direction is $\ker{g_*} \subseteq \operatorname{im}{f_*}$. Let $[b] \in \ker{g_*}$ with $b \in B_n$, so $g(b) \in B(C_n)$, i.e. there exists $c \in C_{n+1}$ such that $g(b) = d(c)$. By exactness of $0 \to A \to B \to C \to 0$ there exists $b' \in B_{n+1}$ such that $g(b') = c$. Because $g$ is a chain map, we have $$g(b) = d(g(b')) = g(d(b')) \implies g(b-d(b')) = 0.$$ Thus, $b-d(b') \in \ker{g}$, so by exactness there exists some $a \in A_n$ with $f(a) = b-d(b')$. But then $f([a]) = [b]$ which shows $[b] \in \operatorname{im}{f_*}$ as desired.
How did I find this proof? I really just followed my nose: I started taking the definition and writing down the only sensible thing one could do at each step. And just after a few lines we came to the desired conclusion!
In fact, it's probably easier to do this yourself than to read the proof of somebody else.
- 9,413
-
1Regarding the first paragraph: One can replace the set-theoretic diagram chase by an arrow-theoretic diagram chase but that's about it. A version of Snake Lemma still has to be proven regardless and I don't think there's a purely abstract way of doing this. – mrtaurho Mar 09 '22 at 16:47
-
2@mrtaurho Depending on what you mean by "purely abstract way", there are purely categorical proofs of the Snake Lemma. But anyway, this question was not about proving the Snake Lemma. – Qi Zhu Mar 10 '22 at 07:33
-
1"Purely abstract" is not the best choice of words I reckon. What kind of categorical proof do you have in mind? – mrtaurho Mar 10 '22 at 10:59
-
1@mrtaurho Honestly, I just remember a tutor presenting a nice proof of the Snake Lemma but not the content haha. Probably something in https://math.stackexchange.com/questions/74871 or https://math.stackexchange.com/questions/314693. – Qi Zhu Mar 11 '22 at 07:17
-
Yeah, that's the arrow-theoretic diagram chase I was refering to (a great account of this can also be found in the later chapters of Aluffi's Algebra: Chapter 0). To be fair, it's pretty abstract all ready. Still "elementary" diagram chases although this might just be the nature of the Snake Lemma :D – mrtaurho Mar 11 '22 at 09:21
-
1@mrtaurho I see. Thanks for the Aluffi reference! :D – Qi Zhu Mar 11 '22 at 09:25
Here's the abstract proof I promised which I guess is the standard proof taught in homological algebra.
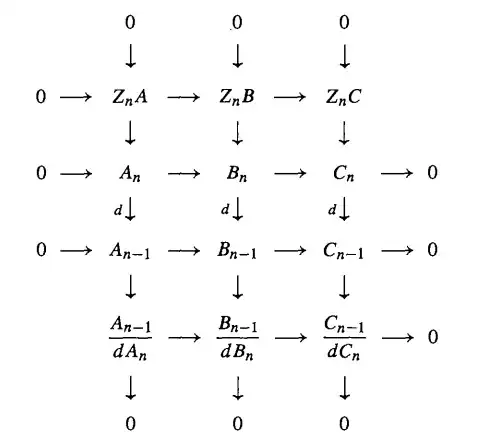
Consider the following commutative diagram which I copied from Weibel (p. 13) because I'm admittingly too lazy to draw a commutative diagram on MSE.
The middle two rows (involving just $A,B,C$) are exact and hence the Snake Lemma shows that the upper and lower row (without the zeros) are exact.
- 9,413