If $f:I\to \mathbb{R}$ is convex and interval $I$ is bounded, prove that $f$ is bounded below.

Question

Let $I$ be a bounded interval and $f:I\to \mathbb{R}$ be a convex function. Prove that $f$ is bounded below in $I.$

Attempt. Let $a,~b\in I$, by convexity of $f$ on $[a,b]:$ $$f(x)\leq g(x):=f(a)+\frac{f(b)-f(a)}{b-a}(x-a)$$ for all $x\in [a,b]$. So it is enough to prove that:

1. $f(x)\geq g(x)$ for $x\in I,~x<a$ or $x>b$,

2. $f$ attains a minimum value $m$ on $[a,b]$,

Thanks for the help.

Answer 1

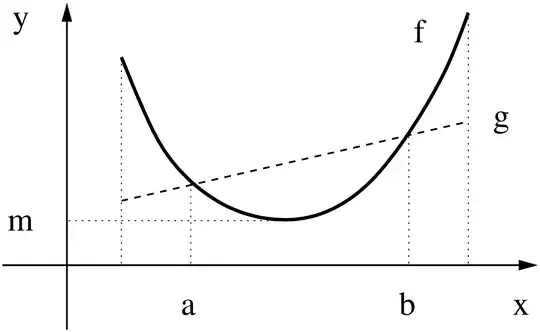
It is easy to show from your first inequality that the upper bound for $f$ on $[a,b]$ is $M = \max(f(a),f(b))$.

To find a lower bound, write $x = \frac{a+b}{2} + \theta$. Since $\frac{a+b}{2} = \frac{1}{2} \left(\frac{a+b}{2} + \theta \right) + \frac{1}{2} \left(\frac{a+b}{2} - \theta \right) $, we have by convexity

$$f\left(\frac{a+b}{2}\right) \leqslant \frac{1}{2}f \left(\frac{a+b}{2} + \theta \right) + \frac{1}{2}f \left(\frac{a+b}{2} - \theta \right),$$

and for all $x \in [a,b]$,

$$f(x) = f\left(\frac{a+b}{2} + \theta \right) \geqslant 2f\left(\frac{a+b}{2}\right)- f \left(\frac{a+b}{2} - \theta \right)$$

But from the upper bound we have $-f \left(\frac{a+b}{2} - \theta \right) \geqslant -M$, and it follows that

$$f(x) \geqslant 2f\left(\frac{a+b}{2}\right)-M = m,$$

providing a lower bound $m$ for $f$ on $[a,b].$

Answer 2

You are almost done. To prove that $f(x)\geq g(x)$ outside $[a,b]$, you can simply do a proof by contradiction.

Then, you still have to prove two things:

1. $g$ is bounded on $I$ (this should be simple due to the nature of $g$).
2. $f$ is bounded on $[a,b]$ (there is a theorem that can help here).