Solution of advanced functional differential equation

Question

Statement

Consider an advanced functional differential equation $$ Lf(x) = f(2x+\pi)+f(2x-\pi),\quad L\equiv\frac{d^2}{dx^2}+1. \tag{1} $$ Let's construct a solution of Eq. $(1)$ with finite support $I\equiv\operatorname{supp}f=\bigl[-\pi,\,\pi\bigr].$

Notation: Denote solution as $\lambda(x),$ i.e. $\lambda(x)\equiv f(x).$

Solution

Applying Fourier transform to $(1)$ after some algebra an expression of a spectrum can be obtained $$ \hat{\lambda}(t)=\prod\limits_{k=0}^{\infty}\frac{\cos\Bigl(\frac{\pi}{2}\cdot t\cdot 2^{-k}\bigr)}{1-(t\cdot 2^{-k})^2}. \tag{2} $$ Expression $(2)$ transforms into a simpler one as well $$ \hat{\lambda}(t) = \operatorname{sinc}(\pi\cdot t)\cdot\prod\limits_{k=0}^{\infty}\frac{1}{1-(t\cdot 2^{-k})^2}. \tag{3} $$ Solution of $(1)$ is defined by inverse Fourier transform $$ \lambda(x)=\frac{1}{2\pi}\int\limits_{\mathbb{R}}e^{itx}\cdot\hat{\lambda}(t)\,dt. \tag{4} $$

Computation

Consider an approximation of $\lambda(x)$ by lacunary Fourier series $$ \lambda(x) = \frac{a_0}{2} + \sum\limits_{k=0}^{\infty}a_{2^k}\cos(2^kx). \tag{5} $$ Note, that $$ a_n = \dfrac{1}{\pi}\int\limits_{I}\lambda(x)\cos(nx)\,dx = \dfrac{1}{\pi}\hat{\lambda}(n). \tag{6} $$ Function $\hat{\lambda}(t)$ does not vanish only at points $n=2^k,\,k=0,1,\ldots,$ and $$ a_{2^k} = \dfrac{1}{\pi}\lim_{t\rightarrow 2^k}\hat{\lambda}(t). \tag{7} $$ Values of first several coefficients are as follows $$ \mathbf{a}=(a_0,\,a_1,\,a_2,\,a_4,\,a_8)=\biggl(\frac1\pi,\,2.3\cdot10^{-1},\,7.7\cdot10^{-2},\,-5.1\cdot10^{-3},\, 8.1\cdot10^{-5},\,-3.2\cdot10^{-7}\biggr) $$

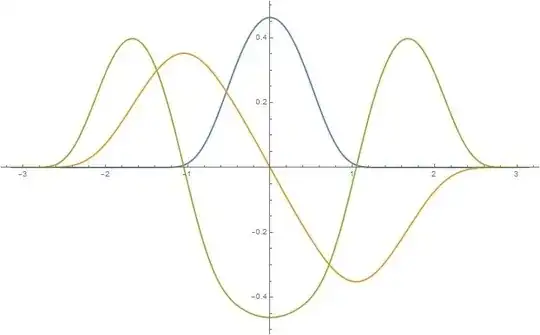
Plot of $\lambda(x)$ graph by $(5)$ with $5$ terms approximation $\mathbf{a}$ is a blue line, first derivative $\lambda'(x)$ (orange), and second derivative $\lambda''(x)$ (green) are shown in the figure

Questions

1. Does a rectangular function function $\chi_{I}(x)$, which is also a characteristic function of the interval $I$ satisfy the Eq. $(1)?$
2. How to construct a fast convergence algorithm to compute values of $f(x)$, like a proposed one?
3. Derivation an exact expression of $a_{2^k}$ in (7)?

Discussion

The problem above is related to the problem of Recursive Integration over Piecewise Polynomials: Closed form? and the form of Eq. (1) close to the Fabius equation.

Reference

Kolodyazhny, V.M., Rvachov, V.A. Cybern Syst Anal (2007) 43: 893 (page 898). DOI: https://doi.org/10.1007/s10559-007-0114-y