7

Given an arbitrary octagon, construct it's midpoint polygon(the midpoint formed by the midpoints of the sides). Erect squares on the sides of the midpoint polygon, all inwards or all outwards. Consider the four segments, each connecting the centroids of two squares corresponding to opposite sides of the midpoint polygon.

The midpoint of these segments form a square.

enter image description here

I distinctly remember seeing this theorem in some geometry article, but I have been unable to find that article. I believe it was attributed to Van Aubel, however I am not too sure. I want to find the source of this theorem because I have found a rather powerful generalisation and I want to revisit that article.

Does anyone find this theorem familiar?

Matthew Conroy
  • 11,334
Tanny Sieben
  • 2,541
  • 1
    Branko Grünbaum (RIP 2018) presented results of this type in a graduate course at the University of Washington many years ago. I'm not sure if they were published outside of lecture notes. There's a wonderful general result that goes something like this: Given an arbitrary $n$-gon, consider the various regular $(n/k)$-gons, defined as having vertices $(\cos 2\pi i k/n,\sin2\pi i k/n)$ for $i=0, 1, \ldots, n-1$. (These include "starry" and "multiply-traced" figures, as well as the "dot" ($k=0$).) [continued] – Blue Jan 03 '19 at 19:37
  • 1
    [continuation] Erecting an $(n/k)$-gon on the sides of the $n$-gon and joining centroids gives a new $n$-gon; erecting some other $(n/k)$-gon on the new sides gives another $n$-gon; etc. Iterating for all-but-one of $(n/k)$-gons, the final polygon is the remaining $(n/k)$-gon. For an $8$-gon, the $(n/k)$-gons are the dot ($k=0$), the regular octagon ($k=1$), the doubly-traced square ($k=2$), "starry octagon" ($k=3$), quad-traced segment ($k=4$, whose derived polygon is a midpoint polygon), and "reverse-direction" versions. Similar to what you have, except for the "opposite sides" thing. – Blue Jan 03 '19 at 19:54
  • @Blue, aren't you describing the Petr-Douglas-Neumann Theorem? ( https://en.wikipedia.org/wiki/Petr-Douglas-Neumann_theorem ) – Tanny Sieben Jan 03 '19 at 20:16
  • 1
    Ah, yes. That seems to be it. – Blue Jan 03 '19 at 20:22
  • 1
    Interestingly, the "opposite sides" thing seems attributable to a common alternative interpretation of $(n/k)$-gon. Rather than starting at $(1,0)$ of a regular "unit" $n$-gon and forming a single (possibly multiply-traced) path by jumping every $k$ vertices, possibly excluding some vertices, we connect every vertex of the $n$ gon to the vertex/vertices $k$ jumps ahead/behind. So, an $(8/4)$-gon would consist of four individual segments (perhaps best thought of as double-traced segments) instead one octo-traced segment. But your figure arguably also uses octo-traced segments. Intriguing. – Blue Jan 03 '19 at 20:37
  • The generalisation I have in mind concerns applying some special transformation(which in this case turns out to be the midpoint transformation) to an arbitrary $nk$-gon, constructing regular $n$-gons on the sides of the newly obtained $nk$-gon, and "collapsing" (in this case the midpoint of opposite sides thing) back to a regular n-gon. The transformation is related to obtaining an affine-regular polygon(in this case, viewing the octogon as an 4*2 gon, you can see that taking the midpoint polygon of a quadrilateral gives you a parallelogram, which is affinely regular) – Tanny Sieben Jan 03 '19 at 20:48
  • A generalization of PDN, seems afoot, as well. Typically, the starting $n$-gon is an $(n/1)$-gon —a cycle— and we erect $(n/k)$-gons whose centroids join into another ostensible $(n/1)$-gon/cycle. The "opposite sides thing" introduces the flexibility of joining centroids to make other $(n/k)$-gons. Your figure amounts to this ad hoc "recipe": $$1,(4),1,(6),4^\star,(4),1 = 2$$ where un-parenthesized #s say which $(n/k)$-gon joins centroids, and parenthesized #s say which $(n/k)$-gon is erected on edges. ($4$ vs $4^\star$ are the two types of $(8/4)$.) Which recipes are "interesting"? – Blue Jan 04 '19 at 00:17
  • 1
    I don't see very much the interest to start from the initial polygon, and then construct a second polygon. Why not start afresh from this second polygon ? – Jean Marie Feb 27 '19 at 22:42

3 Answers3

2

I have a lenghty complex-vector-computational solution. The main idea is in a following lemma.

Lemma: If $ABCD$ is a square with center $S$, then $$ S = {1\over 2}(B-A)i+{1\over 2}(A+B)$$ where letters represent complex numbers of coresponding points (with the same name).

So we get 8 centers and then calculate all $4$ midpoints of those segments. Say we have octagon $ABCDEFGH$, then those midpoints (if we suppose that $A+B+C+D+E+F+G+H =0$) are:

$$ M_1 = {1\over 4}\Big[(D+H-B-F)i+(A+E-C-G)\Big]=-M_3$$ $$ M_2 = {1\over 4}\Big[(A+E-C-G)i+(B+F-D-H)\Big] =-M_4$$

Now it is easy to see that $M_2 = iM_1$ and we are done.

nonuser
  • 91,557
  • 1
    [+1] The approach using complex numbers' geometry is very adapted to such issues. – Jean Marie Feb 27 '19 at 22:44
  • Thank you @JeanMarie, By the way, do you like this one:https://math.stackexchange.com/questions/3126169/stuck-on-a-geometry-puzzle/3126327#3126327 – nonuser Feb 28 '19 at 15:42
  • I didn't accept the answer because I am not looking for a proof (i knew how to prove it beforehand); I was looking for references to publications containing this theorem or similar results. – Tanny Sieben Mar 04 '19 at 18:44
  • No problem, can you post your solution to this problem anyway? – nonuser Mar 04 '19 at 18:49
1

This could be Proposition 9 and Proposition 10 written in Topic "Equilateral Triangle and Kiepert Perspectors in Complex number" written by Dao thanh Oai in Forum Geometricon Volume 15(2015) 105-114.

Proposition 10 (Thebault’s theorem) ´ : Given an octagon $A_1A_2 ··· A_8$, let $B_j$ be the midpoint of $A_jA_j+1$ for indices j = 1, 2,..., 8 (modulo 8). If $C_j$ , j = 1, 2,..., 8, are the centers of the squares on $B_jB_j+1$, all externally or internally of the oc- tagon, then the midpoints of $C_1C_5, C_2C_6, C_3C_7, C_4C_8$ are the vertices of a square.

Note: This above proposition is special case of this given below proposition

Proposition 9 (van Aubel’s theorem). Given an octagon $A_1A_2 ··· A_8$, let $Cj , j$ = 1, 2,..., 8 (indices taken modulo 8) , be the centers of the squares on $A_jA_j+1$, all externally or internally of the octagon. The midpoints of $C_1C_5, C_2C_6, C_3C_7, C_4C_8$ form a quadrilateral with equal and perpendicular diagonals.

  • 3
    While this link may answer the question, it is better to include the essential parts of the answer here and provide the link for reference. Link-only answers can become invalid if the linked page changes. - From Review – José Carlos Santos Mar 10 '22 at 09:29
  • 1
    As it’s currently written, your answer is unclear. Please [edit] to add additional details that will help others understand how this addresses the question asked. You can find more information on how to write good answers in the help center. – Community Mar 10 '22 at 09:29
  • Is my answer is understandable or I have to edit more? –  Mar 10 '22 at 11:40
  • There is one downvote above, please feel free to mention the reason as I have just re-edited the message 1 hour ago. –  Mar 10 '22 at 12:11
  • 1
    This is exactly the article I was looking for all those years back. Thank you! – Tanny Sieben Mar 10 '22 at 20:00
  • @TannySieben, Hi , there is one more interesting answer of Proposition 09 and 10 which could be easily explained by Van Abuel's Theorem. I will not give proof by Algebraic calculation but there are some very simple steps to reduce the proposition 09 and 10 into Van Abuel's Theorem which makes above two proposition obvious.... , Can I Write it as another answer for that , as your questions also ask for "Does anyone find this theorem familiar?" –  Apr 14 '22 at 06:46
  • I simply mean that Proposition 09 and 10 are Equivalent theorem of Van Abuel's Theorem which could be easily explained by some simple steps without Algebraic calculation. –  Apr 14 '22 at 06:55
  • Sure, would be interesting to see! – Tanny Sieben Apr 14 '22 at 16:03
  • @TannySieben , I have mentioned all the steps and try to explain the things in deatail ........., My English is weak so if in any steps or paragraph , you need any further information then let me know. –  Apr 14 '22 at 20:09
0

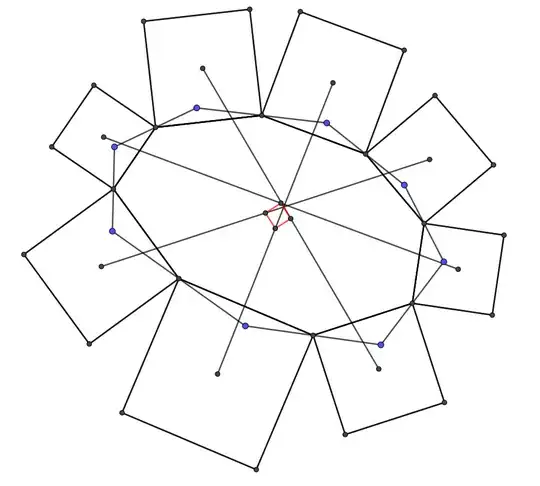
This will be my another possible answer to Claim that Proposition 09 is Equivalent to Van Abuel's Theorem , So follow the Given steps to understand the Situation:

Step 01:Take Two Squares A1A2B1B2 and A9A10B9B10 then m(A2,A10) ;m(A1,A9) ; m(B2,B10); m(B1,B9) makes Green Square as shown in figure: 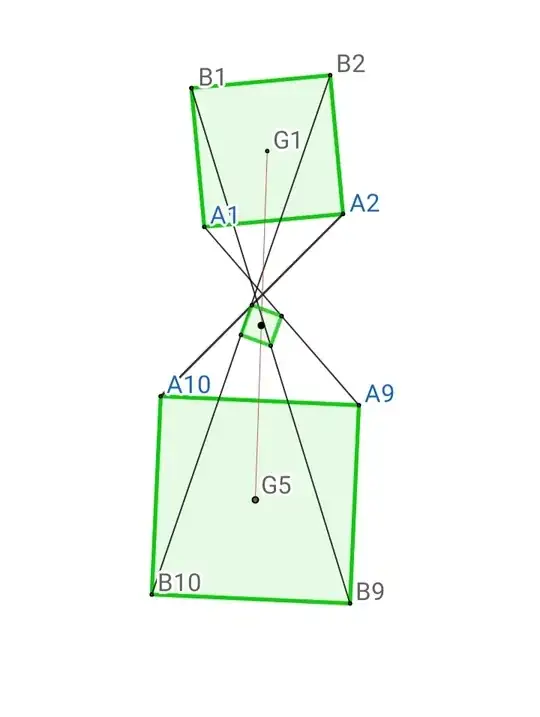van Abuel's Theorem Let G1,G5 be center of Square A1A2B1B2 and A9A10B9B10 then m(G1,G5) will be center of small green Square.

Step 02: We will name small green Square formed in step 01 as "Midpoint of Square A1A2B1B2 and A9A10B9B10".

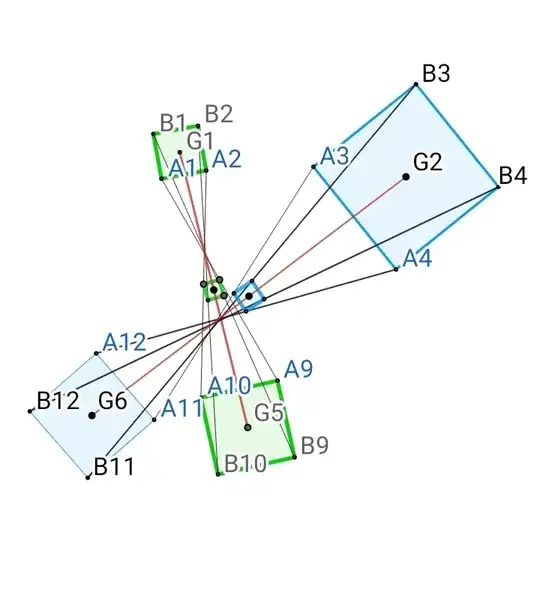
Step03: Similarly make "midpoint of Square of A3A4B3B4 and A11A12B11B12" as Shown in this figure: van Abuel's Theorem

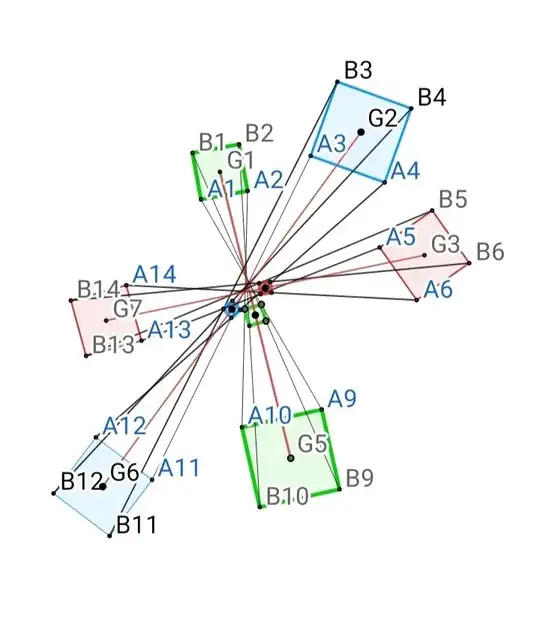
Step04: Now take again "midpoint of Square A5A6B5B6 and A13A14B13B14" as shown in figure: van Abuel's Theorem

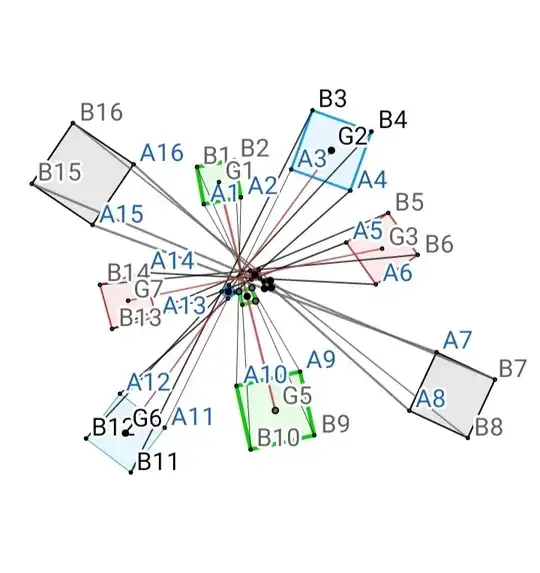
Step 05: Now again take "midpoint of Square A7A8B7B8 and A15A16B15B16" as shown in figure: van Abuel's Theorem

Step 06: When points A2=A3; A4=A5; A6=A7; A8=A9 ; A10=A11 ; A12=A13 ; A14=A15 ; A16=A1 then Figure will looks like this:

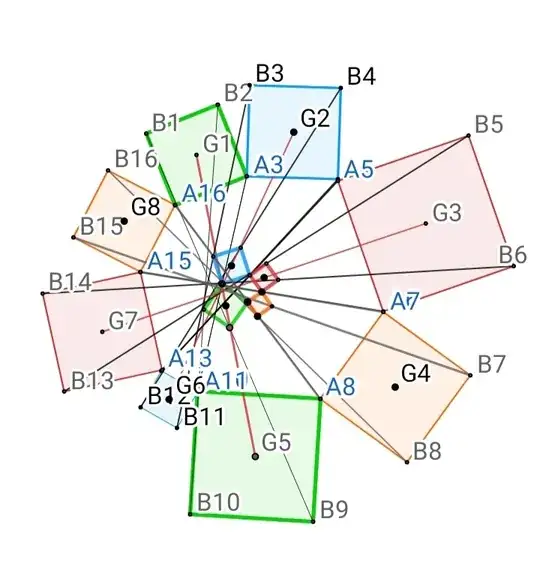
van Abuel's Theorem

Conclusion 01: in steps 01 , we have shown that m(G1,G5) will be center of small green Square and Similarly if we take {G2,G3,....,G8) as center of Squares made on Base {A3A4; A5A6; ......; A15A16} then m(G2,G6);m(G3,G7) ;m(G4,G8) will be center of Squares made in step 03,04,05 and from Van Abuel's Theorem we will understand why those two lines are perpendicular to each other.

Conclusion 02: Proposition 10 is Special case of proposition 09 but question may arise why it becomes a Square?

Solution: The reason is very simple as "*It is well known fact that Centroid of Square made on sides of parallegram in same sence will makes another Square " which is mentioned as Napoleon Barlotti theorem in case of Quadrilateral".

Here is Hint about Where is Parallegram,

Hint= Let A1A2....A8 be convex irregular octagon and Let {C1,C2,....,C8} be m(A1, A2); m(A2,A3); ........; m(A8,A1) then you will find that m(C1,C5) ; m(C2,C6); m(C3,C7);m(C4,C8) makes parallegram as Shown in this figure: van Abuel's Theorem

So from there you Can construct Square on C1C2, C2C3,...,C8C1 and Simillarly Apply all those Steps mentioned above , then you will find that Proposition 10 equivalent to Square mades on Sides of Parallegram!!.