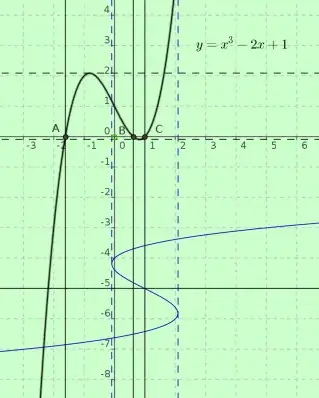
If $P(x)=x^3-2x+1$, define $z_n$ as the number of real roots of the polynomial $P^{\circ n}(x)$, where the superscript denotes $n$-fold composition. Can we find a general formula for $z_n$, or perhaps a recurrence of some sort? The sequence begins $3,7,15,27,47,...$ and is not in the OEIS.
I have solved this problem for the polynomial $Q(x)=x^3-3x+1$, and determined that the number of real zeroes of $Q^{\circ n}$ is equal to $2^{n+1}-1$. However, this problem was much easier because the maximum values of $Q$ occur at integer values of $x$ and the zeroes of $Q$ are irrational, allowing one to break the real line into intervals of the form $[k,k+1]$ and kept track of which intervals $Q$ maps onto one another.
Can anyone figure out how to do this with $P(x)$? This problem has puzzled me for a while, so I am willing to offer a $+50$ bounty for a satisfactory answer or analysis of the problem (as soon as the rules of MSE will allow me to offer it).
It would also be helpful if anyone could provide a large list of values of $z_n$, since all of the values I have were obtained by counting by hand.
Cheers!
EDIT: Should a closed-form formula or recurrence elude any potential answerers, it would also be nice to obtain a (proven) asymptotic formula for $z_n$ instead of a closed-form formula.