1

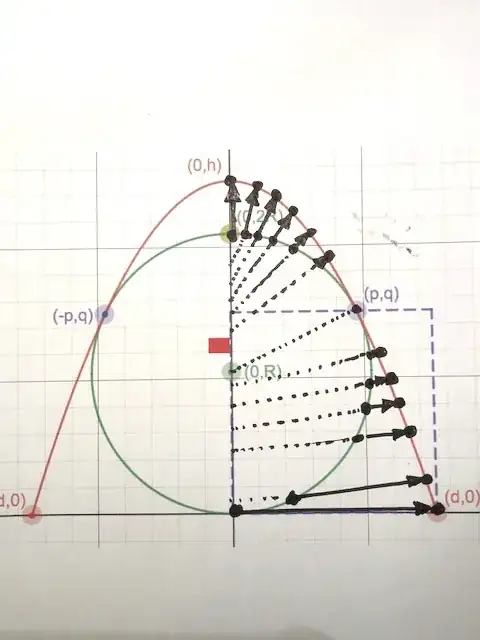
$\hspace{2cm}$enter image description here

Is there a transform that maps points on the circle $$x^2+(y-R)^2=R^2$$ to points on the parabola $$\frac {x^2}{d^2}+\frac y{\frac {d^2}{2(d-R)}}=1$$ as shown by black arrows in the diagram above (and similar for the left side, although not shown in the diagram)?

Note that the parabola touches the circle at $(\pm p,q)$ and these two points map onto themselves.

(See also this question here)

Community
  • 1
Hypergeometricx
  • 23,235
  • 2
    Assuming the origin as projection point of the parabola onto the circle it seems to be possible. – user Sep 13 '18 at 18:52
  • Do you want a curve-to-curve mapping or a deformation of the whole plane ? –  Sep 13 '18 at 18:56
  • 1
    The diagram seems to indicate that the origin would map to both $(d,0)$ and $(-d,0)$ – saulspatz Sep 13 '18 at 18:58
  • I have no idea if this has any validity or not, so take it with a grain of salt: on the existence on this transformation, I'm going to guess that it does exist based only on my knowledge that all conic sections come from the intersection of a cone and a plane. To turn a circle into a parabola, you need a transformation which can both tilt the plane and translate it. Or generalizing your question, you need a transformation which can take any $ax^2 + bxy + cy^2 + dx + ey + f = 0$ to any other equation of degree 2. But I have no idea – DWade64 Sep 13 '18 at 19:03
  • 1
    @DWade64 this is a good idea, but the circle would be projected onto the whole parabola, not only the piece above. In hypergeometric's figure would be the center of this transformation (focus) in the center of the circle. – Viera Čerňanová Sep 13 '18 at 22:29
  • @YvesDaoust - deformation would be useful . – Hypergeometricx Sep 15 '18 at 10:33

2 Answers2

2

Geometrically:

The circle and the parabola can be seen as two sections of the same cone, by two planes having the line $y=q$ in common. The circle is obtained when the plane is orthogonal to the axis, and the parabola when it becomes parallel to a generatrix. This plane is rotated to match the first.

For intermediate rotations, you get ellipses that remain tangent at the same points.

2

There are many ways to do this. Here is one way.

For $-2R\le a\le0$, the equations of the circle and the parabola can be written in the form

  1. $x^2+(y-R)^2=R^2$
  2. $x^2=ay+\left(R-\frac{a}{2}\right)^2$

and the point of intersection will be $(p,q)$ where

$p=\sqrt{R^2-\dfrac{a^2}{4}}$

$q=R-\dfrac{a}{2}$

Define a function $f(x)$ on the interval $[0,p]$ equal to the positive vertical distance between the two curves for $0\le x\le p$:

\begin{equation} f(x)=\frac{1}{a}\left[x^2-\left(R-\frac{a}{2}\right)^2\right]-\left(R+\sqrt{R^2-x^2}\right) \end{equation} and define a function $g(y)$ on the interval $[0,q]$ equal to the positive horizantal distance between the curves for $0\le y\le q$:

\begin{equation} g(y)=\sqrt{ay+\left(R-\frac{a}{2}\right)^2}-\sqrt{R^2-(y-R)^2} \end{equation}

Then for points $(x,y)$ lying on the right half of the circle define the function

\begin{equation} h(x,y)=\begin{cases} (x,y+f(x))\text{ for } 0\le x< p, y> q \\ (x+g(y),y)\text{ for } 0\le y\le q \end{cases} \end{equation} Mapping circle onto parabola

Addendum: Equation 2 above comes from writing the parabolic equation as $x^2=ay+b$ then finding the value of $b$ which gives only one point of intersection with the circle. It is then easy to find both $p$ and $q$ in terms of $R$ and $a$.

John Wayland Bales
  • 22,294