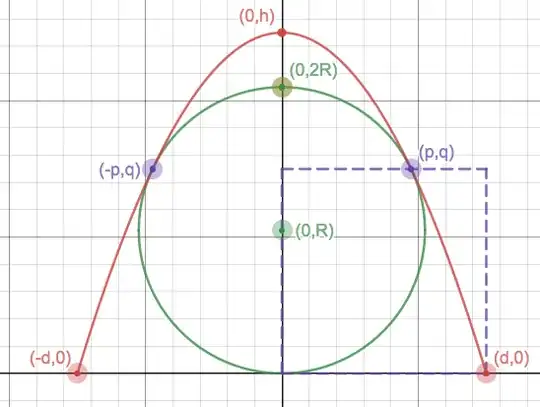
The parabola $\dfrac {x^2}{d^2}+\dfrac yh=1$ touches the circle $x^2+(y-R)^2=R^2$ at two points, $(\pm p, q)$. It can be easily shown geometrically that $p=\sqrt{2qR-q^2}$. Can it be shown geometrically that $q=d$?
See desmos implementation here. The purple dotted line forms a square.
(See also the solution to this other question on projectiles here).
In parabola below, $AM=d$, $VM=h$ and $VF=VN=d^2/(4h)$, where $F$ is the focus and $NH$ the directrix of the parabola. We have $FP=PH$ and $\angle FPC=\angle KPC$, because radius $PC$ is normal to the parabola. Hence $CPHF$ is a parallelogram and $$ CF=PH={h\over d^2} HN^2+VN= {h\over d^2}(FH^2-FN^2)+{d^2\over4h}={h\over d^2}R^2. $$ But $CF=h-R-d^2/(4h)$, which gives: $R=d-d^2/(2h)$. And finally we can compute $q=PK$: $$ PK=h-PH+VN=h-{h\over d^2}R^2+{d^2\over4h}=d. $$
