5

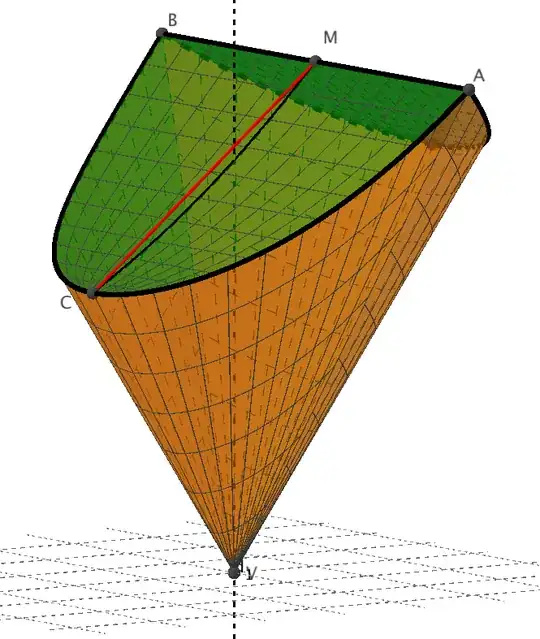
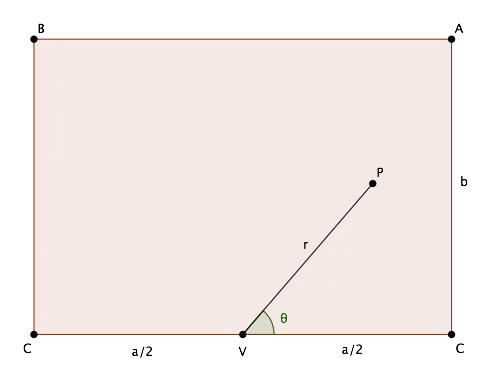
A flexible rectangle sheet size $(a,b),a>b $ is folded half along side $a$ and glued to make a circular cone cut segment of vertex angle $60^{\circ}$ as shown with three edges $(b,a,b).$

( $60^{\circ}$ choice for cone apex angle deformation arises due to maximum volume created by internal pressure at $90^{\circ}$ corner obtained by maintaining second order continuity along a line perpendicular to glue line.)

After bending distorted edges $(a,b)$ are curved/mapped as conical helices with Clairaut minimal radii nearer to cone vertex as $ (r_a,r_b)= (a/4,b).$ The cone surface is a single boat shaped nappe.

Calculate bent area to verify $A= ab $ conserved due to isometry.

Calculate volume enclosed by parallel displacement of edge $AB$ (skew perpendicular to cone axis) along the helices.

It refers to Jack D'Aurizio A4 paper sheet bent volume problem with two nappes.

Isometric Bending of Sheet to Cone

Narasimham
  • 42,260
  • Are you asking for the volume of the convex hull of this surface? – David K Jul 22 '18 at 21:39
  • Yes, if $AB$ is a rubber band then it is the concept of convex hull. (Jack D'Aurizio's problem is different, it asks for holding maximum water at an inclination of cone/ object that may need to be defined). in this case no edges are in a horizontal plane. – Narasimham Jul 22 '18 at 22:56
  • I don't think the resulting solid is convex, because the segment joining the midpoint of $AB$ with the midpoint $C$ or $C'$ of either curve lays outside the solid. The convex hull is simply the solid having for boundaries the cone and planes $ABC$ and $ABC'$. – Intelligenti pauca Jul 23 '18 at 07:07
  • I was imagining lines parallel to $AB$ contacting and sliding along both helices,so that surface has an area $=ab$ – Narasimham Jul 23 '18 at 07:15
  • Why should lines parallel to $AB$ sweep an area $ab$? – Intelligenti pauca Jul 23 '18 at 08:17
  • Thanks for nice sketch. I meant not the new swept area but the original brown conical surface itself that you sketched having area $A=ab$ conserved by isometry i.e. by ,bending to a cone. – Narasimham Jul 23 '18 at 16:38

1 Answers1

4

You can see below a diagram of the solid, made with GeoGebra. Green surface $ABC$ is described by $AB$ sliding along the border: it is apparent from the diagram that segment $CM$ lies over the surface, hence the solid is not convex.

enter image description here

The equation for the lateral surface (orange) can be obtained by noticing that a generic point $P$ on the sheet of paper, having distance $r$ from the midpoint $V$ of the folded side and forming an angle $\angle CVP=\theta$, gets mapped to point $$ P'=\left({1\over2}r\cos2\theta,\ {1\over2}r\sin2\theta,\ {\sqrt3\over2}r \right) $$

of the cone, if we take its axis along $z$ and $V$ as origin.

enter image description here

Intelligenti pauca
  • 55,765