2

Introduction

This question is heavily connected with the related programming aspect around it (link), while the question might be better suited for this stack. However, if it is not suited for this stack just let me know and I will remove it.

Problem/Question

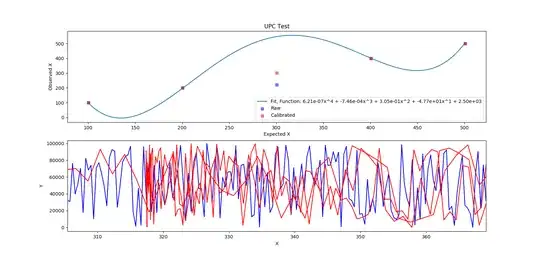
I am trying to calibrate data using a $n$-th degree polynomial using the numpy.polyfit function. The key purpose is to get the best fitting polynomial function that has one $x$-value for any given $y$-value but I am not that strongly versed in the underlying mathematics to understand how I would have to constrain my function to achieve this.

Therefore, the question is if there is some formula/rule that I can use, e.g. every subsequent term should be smaller than the previous term (random thought)?

Example

This would help prevent the problem that arises when a polynomial does have multiple $x$-values for a given $y$-value (first part of plot), namely that the calibrated data has two $y$-values for a given $x$-value (second part of plot). The calibrated $x$-values are acquired by doing new_X = f_polynomial(old_X) for all raw $x$ values.

enter image description here

Addendum

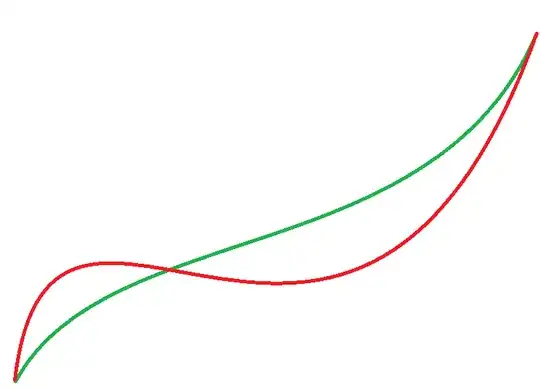
I am trying to constrain a polynomial so that the green variant is valid while the red variant is not valid (two $x$-values for a given $y$-value), with the example using a second third degree polynomial.

enter image description here

Adrian Keister
  • 10,272
Bas Jansen
  • 121
  • looking at your first graph (and not understanding the messier X-Y graph) it seems like using a linear fit (maybe least squares) might be a better idea? – Calvin Khor Jul 09 '18 at 13:51
  • @CalvinKhor You would be right for this test set of data, the key thing is that I am trying to create an algorithm that tries different functions and uses the one that returns the lowest RMS (post calibration). The main part of the second plot is to show that the plot has 2 Y-values for a given X-value between 300 and 500, which is caused by the polynomial having more than 1 X-value for a given Y-value and therefore I am trying to find a way how to restrain a polynomial to always have 1 X- per given Y-value. I hope that this clarifies it a bit? – Bas Jansen Jul 09 '18 at 13:54
  • 3
    It seems that you're looking for polynomials that are one to one? Such polynomials are strictly monotone in $\mathbb{R}$ –  Jul 09 '18 at 14:01
  • Not an answer, but for any set of $n$ points $(x_1,y_1),\dots,(x_n,y_n)$, theres a unique polynomial of degree $n-1$ that passes through it. After this, if you want to make a polynomial of degree $n$, the only thing you can do is adjust it by a multiple of the polynomial $$ \prod_{k=1}^n (x-x_k)$$, and this gives you all such polynomials. – Calvin Khor Jul 09 '18 at 14:04
  • @folouerofkaklas I had never heard of that term before, so thank you just for that. Am I right in taking that the answer than would be to check if my fitted polynomial's derivative has the same sign throughout the region of interest? – Bas Jansen Jul 09 '18 at 14:04
  • Does it have to be a polynomial? Otherwise, you could use monotone cubic interpolation. –  Jul 09 '18 at 14:11
  • @BasJansen yes, thats what strictly monotone would mean. I have no experience with this but perhaps this is useful (it seems to explain Lagrange multipliers with inequality constraints) http://users.wpi.edu/~pwdavis/Courses/MA1024B10/1024_Lagrange_multipliers.pdf – Calvin Khor Jul 09 '18 at 14:12
  • @Rahul The cause of the 'drift' (deviation from expected) has to be caused by a smooth process (e.g. a gradual increase of temperature/pressure or decrease in flowrate), which is why I was trying to use polynomials. – Bas Jansen Jul 09 '18 at 14:12
  • @CalvinKhor Great, I would say that between you and @folouerofkaklas it is apparant that I have to get curve_fit to only try monotone functions. I will now return back to my comfort zone of the actual programming aspect of this, and thank you all for the time it took to figure out what I meant and point me in the right way (i'll accept an answer from either of you that mentions this). – Bas Jansen Jul 09 '18 at 14:16
  • I'll leave it to him, good luck – Calvin Khor Jul 09 '18 at 14:17
  • 1
    If you run into trouble doing curve fitting on monotonic polynomials, remember that a monotone cubic spline is also smooth and is easy to compute. –  Jul 09 '18 at 14:22
  • 1
    One sufficient condition would be to check that the derivative of the polynomial has no roots in the range of values of interest. – copper.hat Jul 09 '18 at 14:24
  • @Rahul I have noted it and was looking at it earlier, it's something I need to digest first before I can make any comment on it but thank you for pointing me to a new concept. – Bas Jansen Jul 09 '18 at 14:24
  • 1
    Check this answer: https://math.stackexchange.com/questions/60610/polynomial-fitting-where-polynomial-must-be-monotonically-increasing. – Adrian Keister Jul 09 '18 at 14:46
  • @BasJansen I've peeked at your code a little, and at the part where you loop over degrees and run polyfit, if you are prepared to use a polynomial of high degree, there is no reason to run the loop. Allowing yourself to use a degree $n-1$ polynomial will always allow you to perfectly interpolate the points (with a unique polynomial, so there's no freedom on the gradients), which will make the RMS error 0. If you are then allowing yourself a degree $n$ polynomial you have a vector space of solutions of dimension 1 which may allow you to find something matching your constraint – Calvin Khor Jul 09 '18 at 15:25

0 Answers0